Question

If $\sqrt[3]{a} + \sqrt[3]{b} + \sqrt[3]{c} = 0$ and $(a + b + c)^3 =$

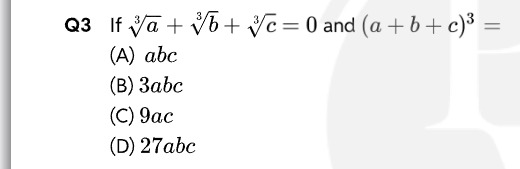
• A. abc
• B. 3abc
• C. 9ac
• D. 27abc

Answer 1

Answer: (D)

27abc

Answer 2

Using the identity for three terms:

$$(x+y+z)^3 = x^3 + y^3 + z^3 + 3(x+y)(y+z)(z+x).$$

Let $x = \sqrt[3]{a},\, y = \sqrt[3]{b},\, z = \sqrt[3]{c}$.
Since $x+y+z=0$, we have

$$x^3+y^3+z^3 = 3xyz.$$

That is,

$$a + b + c = 3\sqrt[3]{abc}.$$

Cubing both sides gives

$$(a+b+c)^3 = 27\,abc.$$