Solveeit Logo
Login

Question

Question: If $\lim_{x \to 1^+} \frac{(x-1)(6+\lambda \cos(x-1))+\mu \sin(1-x)}{(x-1)^3} = -1$, where $\lambda,...

If lim⁡x→1+(x−1)(6+λcos⁡(x−1))+μsin⁡(1−x)(x−1)3=−1\lim_{x \to 1^+} \frac{(x-1)(6+\lambda \cos(x-1))+\mu \sin(1-x)}{(x-1)^3} = -1, where λ,μ∈R\lambda, \mu \in \mathbb{R}, then λ+μ\lambda + \mu is equal to

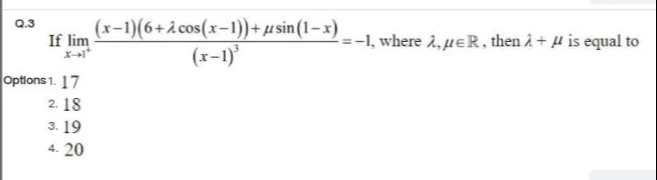
A

17

B

18

C

19

D

20

Answer

18

Explanation

Solution

We substitute h=x−1h = x-1 so that as x→1+x\to1^+, h→0+h\to0^+. The expression becomes:

h(6+λcos⁡h)+μsin⁡(1−x)h3\frac{h\left(6+\lambda \cos h\right) + \mu \sin(1-x)}{h^3}

Since sin⁡(1−x)=sin⁡(−h)=−sin⁡h\sin(1-x)=\sin(-h)=-\sin h, the numerator transforms to:

h(6+λcos⁡h)−μsin⁡hh\left(6+\lambda\cos h\right) - \mu \sin h

Step 1: Taylor Series Expansion

For small hh,

cos⁡h=1−h22+O(h4),sin⁡h=h−h36+O(h5)\cos h = 1-\frac{h^2}{2}+O(h^4),\quad \sin h = h-\frac{h^3}{6}+O(h^5)

Step 2: Substitute the series into the numerator

h(6+λ(1−h22))−μ(h−h36)=6h+λh−λ2h3−μh+μ6h3=(6+λ−μ)h+(−λ2+μ6)h3\begin{aligned} h\left(6+\lambda\left(1-\frac{h^2}{2}\right)\right) - \mu\left(h-\frac{h^3}{6}\right) &= 6h + \lambda h - \frac{\lambda}{2}h^3 - \mu h + \frac{\mu}{6}h^3\\[1mm] &= \left(6+\lambda-\mu\right)h + \left(-\frac{\lambda}{2}+\frac{\mu}{6}\right)h^3 \end{aligned}

Step 3: For the limit to be finite

The coefficient of hh must be zero:

6+λ−μ=0⟹μ=6+λ.6+\lambda-\mu=0\quad \Longrightarrow \quad \mu = 6+\lambda.

Now the numerator simplifies to:

(−λ2+μ6)h3.\left(-\frac{\lambda}{2}+\frac{\mu}{6}\right)h^3.

Taking the limit,

lim⁡h→0(−λ2+μ6)h3h3=−λ2+μ6=−1.\lim_{h\to0}\frac{\left(-\frac{\lambda}{2}+\frac{\mu}{6}\right)h^3}{h^3} = -\frac{\lambda}{2}+\frac{\mu}{6} = -1.

Step 4: Substitute μ=6+λ\mu = 6+\lambda and solve

−λ2+6+λ6=−1.-\frac{\lambda}{2}+\frac{6+\lambda}{6}=-1.

Multiply both sides by 6:

−3λ+6+λ=−6.-3\lambda +6+\lambda = -6. −2λ+6=−6.-2\lambda +6 = -6. −2λ=−12⟹λ=6.-2\lambda = -12 \quad \Longrightarrow \quad \lambda = 6.

Then,

μ=6+λ=6+6=12.\mu = 6+\lambda = 6+6 = 12.

Thus,

λ+μ=6+12=18.\lambda+\mu = 6+12 = 18.