Question
Question: Charge on the capacitor in the given circuit in steady state condition is ...
Charge on the capacitor in the given circuit in steady state condition is
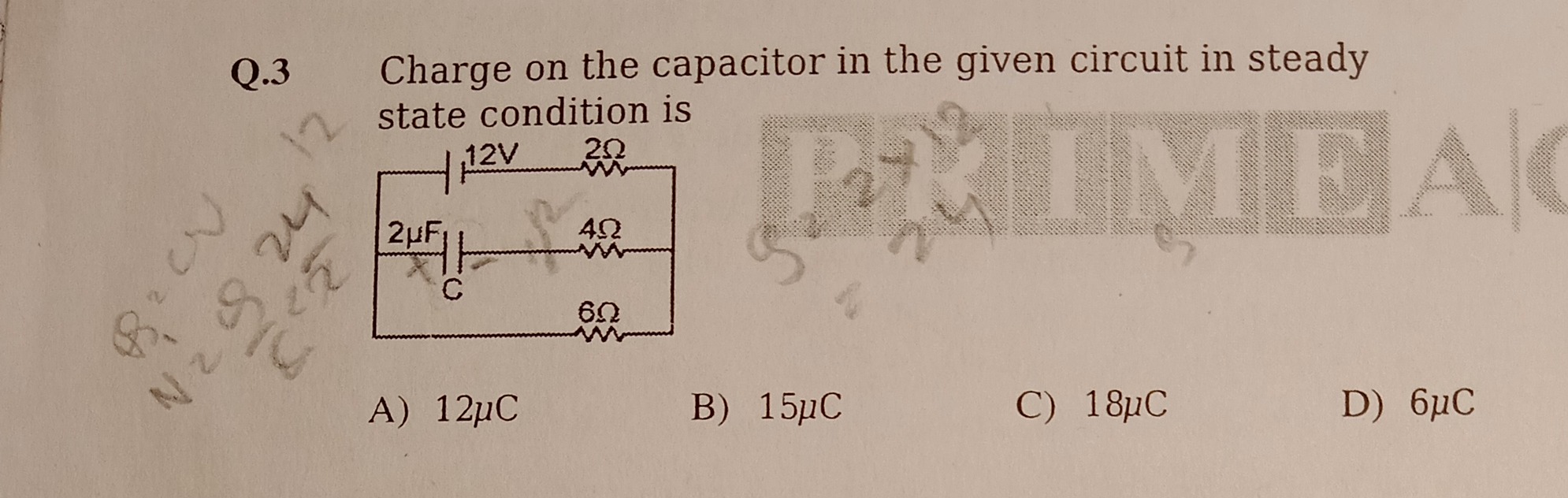
12μC
15μC
18μC
6μC
18μC
Solution
1. Understanding Steady State in DC Circuits:
In a DC circuit, at steady state, a capacitor acts as an open circuit. This means that no current flows through the branch containing the capacitor.
2. Simplifying the Circuit at Steady State:
Given the circuit diagram:
- A 12V voltage source is connected in series with a 2Ω resistor.
- After the 2Ω resistor, the circuit branches into two parallel paths:
- Path 1: A 4Ω resistor in series with a 2μF capacitor.
- Path 2: A 6Ω resistor.
- These two paths then rejoin and connect back to the negative terminal of the 12V source.
Since the capacitor acts as an open circuit in steady state, no current flows through Path 1 (the branch containing the 4Ω resistor and the 2μF capacitor). Therefore, the 4Ω resistor is effectively out of the main current path.
The current from the 12V source will flow through the 2Ω resistor and then entirely through the 6Ω resistor. This means the 2Ω resistor and the 6Ω resistor are effectively in series.
3. Calculating the Total Current:
The total equivalent resistance (Req) of the circuit for current flow is the sum of the series resistances:
Req=2Ω+6Ω=8Ω
Using Ohm's Law, the total current (I) flowing from the battery is:
I=ReqV=8Ω12V=1.5A
4. Determining the Voltage Across the Capacitor:
The capacitor (in series with the 4Ω resistor) is connected in parallel with the 6Ω resistor. The voltage across any parallel branch is the same. Therefore, the voltage across the capacitor branch is equal to the voltage across the 6Ω resistor.
The voltage across the 6Ω resistor (V6Ω) is:
V6Ω=I×6Ω=1.5A×6Ω=9V
Since no current flows through the 4Ω resistor (because the capacitor branch is open), there is no voltage drop across the 4Ω resistor. This means the entire voltage across the parallel combination (which is 9V) appears across the capacitor. So, the voltage across the capacitor (VC) is 9V.
5. Calculating the Charge on the Capacitor:
The charge (Q) on a capacitor is given by the formula:
Q=C×VC Given capacitance C=2μF=2×10−6F. Calculated voltage VC=9V.
Q=(2×10−6F)×9V=18×10−6C=18μC
