Question

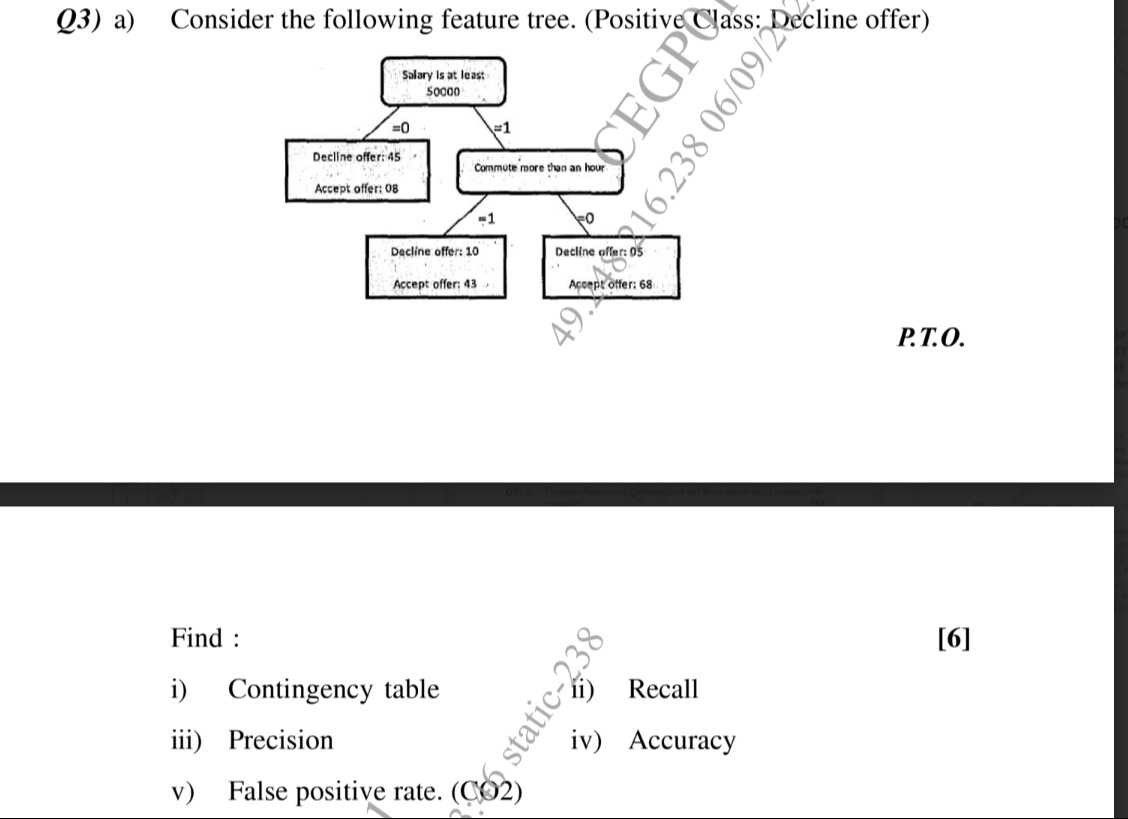
Q3) a) Consider the following feature tree. (Positive Class: Decline offer)

Find : i) Contingency table ii) Recall iii) Precision iv) Accuracy v) False positive rate. (CO2) [6] P.T.O.

Answer 1

i) Contingency table:

	Predicted Decline Offer	Predicted Accept Offer
Actual Decline Offer	45	15
Actual Accept Offer	8	111

ii) Recall = 0.75 iii) Precision ≈ 0.8491 iv) Accuracy ≈ 0.8715 v) False Positive Rate ≈ 0.0672

Answer 2

To solve this problem, we first need to extract the True Positives (TP), True Negatives (TN), False Positives (FP), and False Negatives (FN) from the given feature tree.

The Positive Class is defined as "Decline offer". The Negative Class is "Accept offer".

A decision tree makes a prediction for instances that fall into a leaf node. The prediction is typically the majority class within that leaf node.

Let's analyze each leaf node:

1. Left Leaf Node (Salary < 50000):

• "Decline offer: 45"
• "Accept offer: 08" The majority class here is "Decline offer" (45 > 8). So, the model predicts "Decline offer" for all instances reaching this node.
• True Positives (TP): Instances correctly predicted as "Decline offer" (actual "Decline offer"). From this node: 45
• False Positives (FP): Instances incorrectly predicted as "Decline offer" (actual "Accept offer"). From this node: 8

2. Right-Left Leaf Node (Salary >= 50000 AND Commute > 1 hour):

• "Decline offer: 10"
• "Accept offer: 43" The majority class here is "Accept offer" (43 > 10). So, the model predicts "Accept offer" for all instances reaching this node.
• False Negatives (FN): Instances incorrectly predicted as "Accept offer" (actual "Decline offer"). From this node: 10
• True Negatives (TN): Instances correctly predicted as "Accept offer" (actual "Accept offer"). From this node: 43

3. Right-Right Leaf Node (Salary >= 50000 AND Commute <= 1 hour):

• "Decline offer: 05"
• "Accept offer: 68" The majority class here is "Accept offer" (68 > 5). So, the model predicts "Accept offer" for all instances reaching this node.
• False Negatives (FN): Instances incorrectly predicted as "Accept offer" (actual "Decline offer"). From this node: 5
• True Negatives (TN): Instances correctly predicted as "Accept offer" (actual "Accept offer"). From this node: 68

Now, let's aggregate these values:

• Total True Positives (TP) = 45
• Total False Positives (FP) = 8
• Total False Negatives (FN) = 10 + 5 = 15
• Total True Negatives (TN) = 43 + 68 = 111

Total number of instances = TP + FP + FN + TN = 45 + 8 + 15 + 111 = 179

Now we can calculate the required metrics:

i) Contingency table (Confusion Matrix): The contingency table summarizes the performance:

	Predicted Decline Offer (Positive)	Predicted Accept Offer (Negative)	Total Predicted
Actual Decline Offer (Positive)	45 (TP)	15 (FN)	60
Actual Accept Offer (Negative)	8 (FP)	111 (TN)	119
Total Actual	53	126	179

ii) Recall (Sensitivity or True Positive Rate): Recall measures the proportion of actual positive cases that were correctly identified. $\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} = \frac{45}{45 + 15} = \frac{45}{60} = 0.75$

iii) Precision (Positive Predictive Value): Precision measures the proportion of positive predictions that were actually correct. $\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} = \frac{45}{45 + 8} = \frac{45}{53} \approx 0.8491$

iv) Accuracy: Accuracy measures the proportion of total predictions that were correct. $\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{FP} + \text{FN} + \text{TN}} = \frac{45 + 111}{45 + 8 + 15 + 111} = \frac{156}{179} \approx 0.8715$

v) False Positive Rate (FPR) (Fall-out): FPR measures the proportion of actual negative cases that were incorrectly identified as positive. $\text{False Positive Rate} = \frac{\text{FP}}{\text{FP} + \text{TN}} = \frac{8}{8 + 111} = \frac{8}{119} \approx 0.0672$

Explanation of the solution:

1. Identify TP, FP, FN, TN: From each leaf node, determine the predicted class (majority class) and then classify the actual counts into True Positives (TP), False Positives (FP), False Negatives (FN), and True Negatives (TN) based on the "Decline offer" being the positive class.
   • Leaf 1 (Salary < 50000): Predicted "Decline offer". Actual "Decline offer" (45) are TP; Actual "Accept offer" (8) are FP.
   • Leaf 2 (Salary >= 50000 AND Commute > 1 hour): Predicted "Accept offer". Actual "Decline offer" (10) are FN; Actual "Accept offer" (43) are TN.
   • Leaf 3 (Salary >= 50000 AND Commute <= 1 hour): Predicted "Accept offer". Actual "Decline offer" (5) are FN; Actual "Accept offer" (68) are TN.
2. Aggregate counts: Sum up TP, FP, FN, TN from all leaf nodes.
   • TP = 45
   • FP = 8
   • FN = 10 + 5 = 15
   • TN = 43 + 68 = 111
3. Calculate metrics: Apply the standard formulas for each required metric using the aggregated counts.