Question

The angle of projection of a particle is measured from the vertical axis as $\phi$ and the maximum height reached by the particle is $h_m$. Here $h_m$ as function of $\phi$ can be presented as

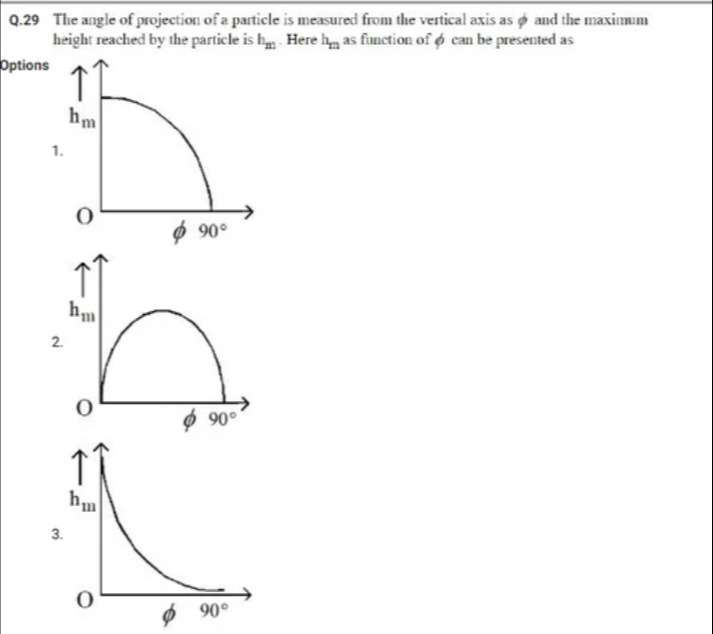
• A. A graph with the x-axis labeled as $\phi$ and ranging from 0 to 90 degrees, and the y-axis labeled as $h_m$. The curve starts at $h_m$ when $\phi$ is 0 degrees and decreases to 0 when $\phi$ is 90 degrees. The curve appears to be a quarter circle. The origin is labeled as O. An arrow points upwards next to $h_m$.
• B. A graph with the x-axis labeled as $\phi$ and ranging from 0 to 90 degrees, and the y-axis labeled as $h_m$. The curve starts at 0 when $\phi$ is 0 degrees, increases to a maximum value, and decreases to 0 when $\phi$ is 90 degrees. The curve appears to be a half circle. The origin is labeled as O. An arrow points upwards next to $h_m$.
• C. A graph with the x-axis labeled as $\phi$ and ranging from 0 to 90 degrees, and the y-axis labeled as $h_m$. The curve starts at $h_m$ when $\phi$ is 0 degrees and decreases to 0 when $\phi$ is 90 degrees. The curve appears to be an exponential decay. The origin is labeled as O. An arrow points upwards next to $h_m$.

Answer 1

Answer: (A)

Option 1

Answer 2

The maximum height for a projectile when the projection angle is measured from the vertical is given by:

$h = \frac{(u\cos\phi)^2}{2g} = h_m\,\cos^2\phi$,

where

$h_m = \frac{u^2}{2g}$.

Thus, $h$ as a function of $\phi$ is proportional to $\cos^2 \phi$. This function has its maximum value $h_m$ at $\phi=0^\circ$ and decreases gradually to 0 at $\phi=90^\circ$.

Core Explanation:
The maximum height is $h = h_m \cos^2\phi$. It is maximum at $\phi = 0^\circ$ (equal to $h_m$) and zero at $\phi = 90^\circ$. Option 1 correctly captures this behavior.