Question
Question: Find the ratio in which area enclosed by y = cosx, x-axis, x = 0, x = $\pi$/2, is divided by the cur...
Find the ratio in which area enclosed by y = cosx, x-axis, x = 0, x = π/2, is divided by the curve y = sinx.
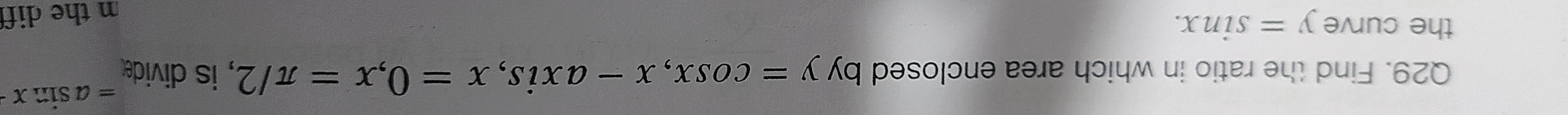
1:2
Solution
The problem asks us to find the ratio in which the area enclosed by y=cosx, the x-axis, x=0, and x=π/2 is divided by the curve y=sinx.
1. Calculate the total area: The total area, let's call it Atotal, is the area under the curve y=cosx from x=0 to x=π/2. Since cosx≥0 in this interval, the area is: Atotal=∫0π/2cosxdx Atotal=[sinx]0π/2 Atotal=sin(π/2)−sin(0) Atotal=1−0=1 square unit.
2. Understand how the curve y=sinx divides the area: Let's visualize the curves y=sinx and y=cosx in the interval [0,π/2].
- At x=0, cosx=1, sinx=0.
- At x=π/2, cosx=0, sinx=1.
- The curves intersect when sinx=cosx, which occurs at x=π/4 in this interval. At this point, sin(π/4)=cos(π/4)=1/2.
The total area Atotal is the region R={(x,y)∣0≤x≤π/2,0≤y≤cosx}. The curve y=sinx divides this region R into two parts:
- Part 1 (A1): The area of the region R that lies below or on the curve y=sinx.
- Part 2 (A2): The area of the region R that lies above the curve y=sinx.
Let's determine the boundaries for A1 and A2:
For Part 1 (A1): This area is bounded by y=min(cosx,sinx) and the x-axis.
- For 0≤x≤π/4, sinx≤cosx, so min(cosx,sinx)=sinx.
- For π/4≤x≤π/2, cosx≤sinx, so min(cosx,sinx)=cosx.
So, A1=∫0π/4sinxdx+∫π/4π/2cosxdx. A1=[−cosx]0π/4+[sinx]π/4π/2 A1=(−cos(π/4)−(−cos(0)))+(sin(π/2)−sin(π/4)) A1=(−1/2+1)+(1−1/2) A1=2−2/2=2−2.
For Part 2 (A2): This area is bounded by y=cosx (upper curve) and y=sinx (lower curve). This region exists only where sinx≤cosx, which is for 0≤x≤π/4. So, A2=∫0π/4(cosx−sinx)dx. A2=[sinx+cosx]0π/4 A2=(sin(π/4)+cos(π/4))−(sin(0)+cos(0)) A2=(1/2+1/2)−(0+1) A2=2/2−1=2−1.
3. Verify the sum of areas: A1+A2=(2−2)+(2−1)=1. This matches Atotal, confirming our calculations and interpretation.
4. Find the ratio: The question asks for the ratio in which the area is divided. This usually means the ratio of the two parts. We have A1=2−2 and A2=2−1. Numerically, A1≈2−1.414=0.586 and A2≈1.414−1=0.414. So A2 is the smaller part and A1 is the larger part. The ratio is commonly expressed as smaller to larger.
Ratio = A2:A1=(2−1):(2−2) To simplify the ratio, divide both sides by (2−1): Ratio = 1:2−12−2 2−12−2=2−12(2−1)=2.
So, the ratio is 1:2.
