Question

Find the co-ordinates of the incentre of the triangle formed by the line x + y+1=0; x-y+3=0 & 7x-y+3=0. Also find the centre of the circle escribed to 7x-y+3 = 0.

Answer 1

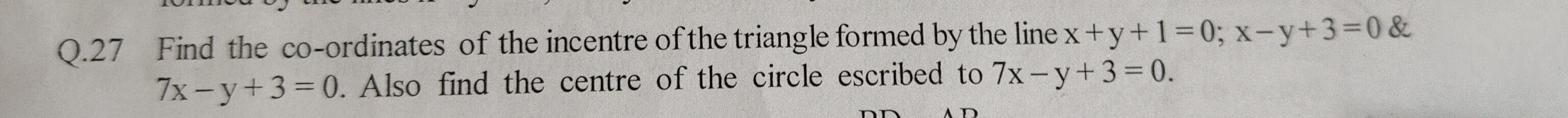
The co-ordinates of the incentre are (-1, 1) and the centre of the circle escribed to 7x-y+3 = 0 is (4, 1).

Answer 2

The three lines forming the triangle are: $L_1: x + y + 1 = 0$ $L_2: x - y + 3 = 0$ $L_3: 7x - y + 3 = 0$

1. Finding the Vertices of the Triangle

• Vertex A (Intersection of $L_1$ and $L_2$): Adding $L_1$ and $L_2$: $(x+y+1) + (x-y+3) = 0 \implies 2x + 4 = 0 \implies x = -2$. Substituting $x=-2$ into $L_1$: $-2 + y + 1 = 0 \implies y = 1$. Vertex A is $(-2, 1)$.

• Vertex B (Intersection of $L_1$ and $L_3$): From $L_1$, $y = -x - 1$. Substituting into $L_3$: $7x - (-x - 1) + 3 = 0 \implies 8x + 4 = 0 \implies x = -1/2$. Substituting $x=-1/2$ into $y = -x - 1$: $y = -(-1/2) - 1 = -1/2$. Vertex B is $(-1/2, -1/2)$.

• Vertex C (Intersection of $L_2$ and $L_3$): From $L_2$, $y = x + 3$. Substituting into $L_3$: $7x - (x + 3) + 3 = 0 \implies 6x = 0 \implies x = 0$. Substituting $x=0$ into $y = x + 3$: $y = 3$. Vertex C is $(0, 3)$.

The vertices are A$(-2, 1)$, B$(-1/2, -1/2)$, and C$(0, 3)$.

2. Finding the Lengths of the Sides

Let $a$ be the length of the side opposite Vertex A (BC), $b$ opposite Vertex B (AC), and $c$ opposite Vertex C (AB).

• $a = BC = \sqrt{(0 - (-1/2))^2 + (3 - (-1/2))^2} = \sqrt{(1/2)^2 + (7/2)^2} = \sqrt{1/4 + 49/4} = \sqrt{50/4} = \frac{5\sqrt{2}}{2}$.
• $b = AC = \sqrt{(0 - (-2))^2 + (3 - 1)^2} = \sqrt{2^2 + 2^2} = \sqrt{8} = 2\sqrt{2}$.
• $c = AB = \sqrt{(-1/2 - (-2))^2 + (-1/2 - 1)^2} = \sqrt{(3/2)^2 + (-3/2)^2} = \sqrt{9/4 + 9/4} = \sqrt{18/4} = \frac{3\sqrt{2}}{2}$.

3. Finding the Incenter

The incenter $I$ is given by $I = \left( \frac{ax_A + bx_B + cx_C}{a+b+c}, \frac{ay_A + by_B + cy_C}{a+b+c} \right)$. Sum of side lengths: $a+b+c = \frac{5\sqrt{2}}{2} + 2\sqrt{2} + \frac{3\sqrt{2}}{2} = 6\sqrt{2}$.

Numerator for x-coordinate: $ax_A + bx_B + cx_C = \frac{5\sqrt{2}}{2}(-2) + 2\sqrt{2}(-1/2) + \frac{3\sqrt{2}}{2}(0) = -5\sqrt{2} - \sqrt{2} = -6\sqrt{2}$. Numerator for y-coordinate: $ay_A + by_B + cy_C = \frac{5\sqrt{2}}{2}(1) + 2\sqrt{2}(-1/2) + \frac{3\sqrt{2}}{2}(3) = \frac{5\sqrt{2}}{2} - \sqrt{2} + \frac{9\sqrt{2}}{2} = 6\sqrt{2}$.

Incenter coordinates: $I = \left( \frac{-6\sqrt{2}}{6\sqrt{2}}, \frac{6\sqrt{2}}{6\sqrt{2}} \right) = (-1, 1)$.

4. Finding the Center of the Escribed Circle

The circle escribed to the line $7x-y+3=0$ (which is $L_3$) has its center at the excenter opposite to the side $L_3$. This side $L_3$ is opposite to Vertex A. Therefore, we need to find the excenter $I_A$.

The formula for the excenter $I_A$ (opposite to vertex A) is: $I_A = \left( \frac{-ax_A + bx_B + cx_C}{-a+b+c}, \frac{-ay_A + by_B + cy_C}{-a+b+c} \right)$

Denominator: $-a+b+c = -\frac{5\sqrt{2}}{2} + 2\sqrt{2} + \frac{3\sqrt{2}}{2} = \frac{-5\sqrt{2} + 4\sqrt{2} + 3\sqrt{2}}{2} = \frac{2\sqrt{2}}{2} = \sqrt{2}$.

Numerator for x-coordinate: $-ax_A + bx_B + cx_C = -(\frac{5\sqrt{2}}{2})(-2) + (2\sqrt{2})(-1/2) + (\frac{3\sqrt{2}}{2})(0) = 5\sqrt{2} - \sqrt{2} = 4\sqrt{2}$. Numerator for y-coordinate: $-ay_A + by_B + cy_C = -(\frac{5\sqrt{2}}{2})(1) + (2\sqrt{2})(-1/2) + (\frac{3\sqrt{2}}{2})(3) = -\frac{5\sqrt{2}}{2} - \sqrt{2} + \frac{9\sqrt{2}}{2} = \frac{-5\sqrt{2} - 2\sqrt{2} + 9\sqrt{2}}{2} = \frac{2\sqrt{2}}{2} = \sqrt{2}$.

Excenter $I_A$ coordinates: $I_A = \left( \frac{4\sqrt{2}}{\sqrt{2}}, \frac{\sqrt{2}}{\sqrt{2}} \right) = (4, 1)$.

Conclusion: The co-ordinates of the incentre are $(-1, 1)$. The centre of the circle escribed to $7x-y+3=0$ is $(4, 1)$.