Question

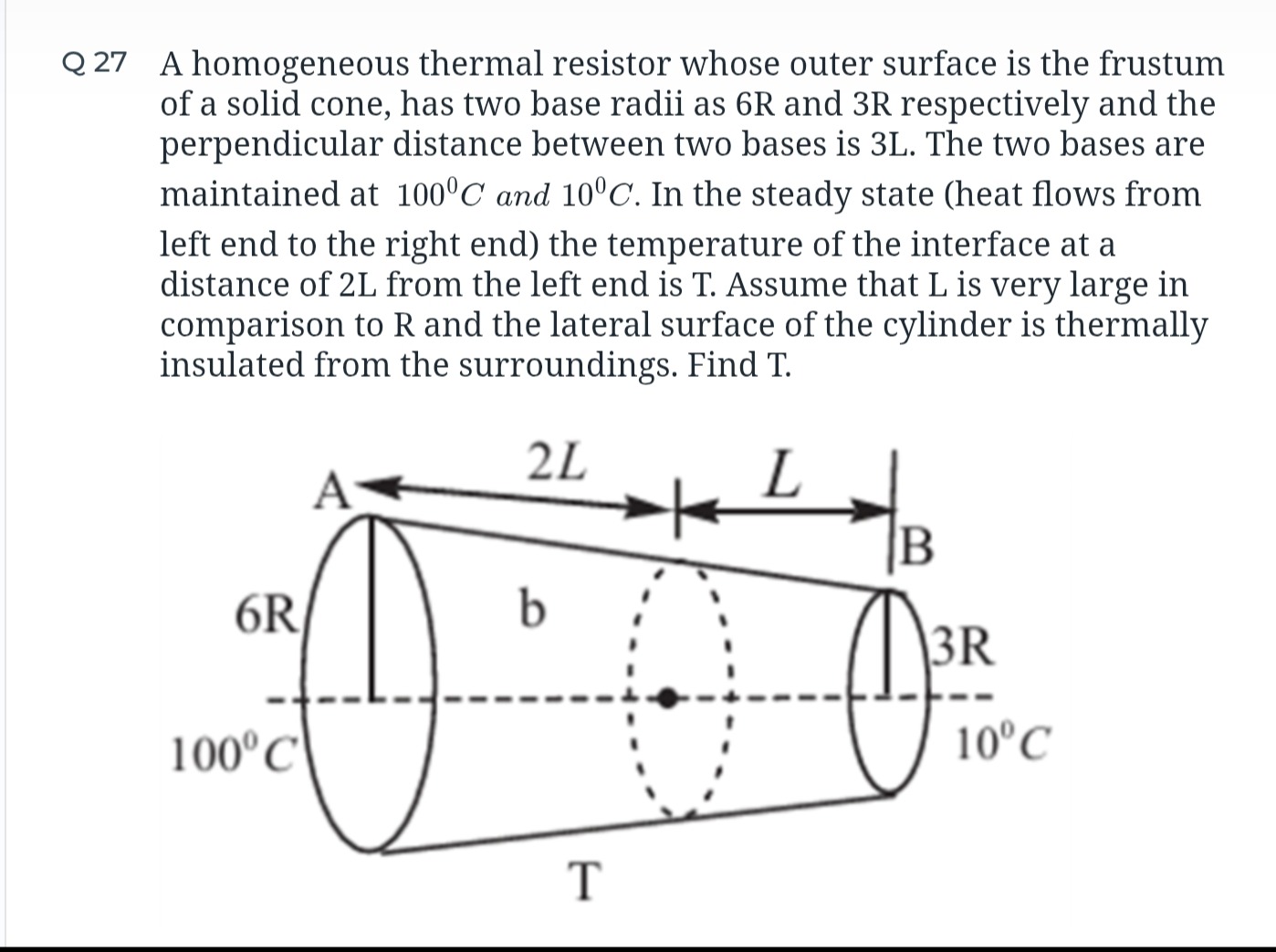
A homogeneous thermal resistor whose outer surface is the frustum of a solid cone, has two base radii as 6R and 3R respectively and the perpendicular distance between two bases is 3L. The two bases are maintained at $100^0C$ and $10^0C$. In the steady state (heat flows from left end to the right end) the temperature of the interface at a distance of 2L from the left end is T. Assume that L is very large in comparison to R and the lateral surface of the cylinder is thermally insulated from the surroundings. Find T.

• A. 55
• B. 60
• C. 70
• D. 75

Answer 1

Answer: (A)

55

Answer 2

In steady state, the rate of heat flow ($Q$) is constant. The radius of the frustum at a distance $x$ from the left end is $r(x) = 6R - \frac{R}{L}x$. The cross-sectional area is $A(x) = \pi r(x)^2$. The heat flow equation is $Q = -kA(x) \frac{dT}{dx}$.

Integrating from $x=0$ ($T_1 = 100^\circ C$) to $x=2L$ (T): $\int_{100}^{T} dT = -\frac{Q}{k\pi} \int_{0}^{2L} \frac{dx}{(6R - \frac{R}{L}x)^2}$ $T - 100 = -\frac{Q}{k\pi} \left[ \frac{L}{R} \frac{1}{6R - \frac{R}{L}x} \right]_0^{2L}$ $T - 100 = -\frac{QL}{k\pi R} \left( \frac{1}{4R} - \frac{1}{6R} \right) = -\frac{QL}{k\pi R} \left( \frac{3-2}{12R} \right) = -\frac{QL}{12k\pi R^2}$ (1)

Integrating from $x=2L$ (T) to $x=3L$ ($T_2 = 10^\circ C$): $\int_{T}^{10} dT = -\frac{Q}{k\pi} \int_{2L}^{3L} \frac{dx}{(6R - \frac{R}{L}x)^2}$ $10 - T = -\frac{Q}{k\pi} \left[ \frac{L}{R} \frac{1}{6R - \frac{R}{L}x} \right]_{2L}^{3L}$ $10 - T = -\frac{QL}{k\pi R} \left( \frac{1}{3R} - \frac{1}{4R} \right) = -\frac{QL}{k\pi R} \left( \frac{4-3}{12R} \right) = -\frac{QL}{12k\pi R^2}$ (2)

Equating (1) and (2): $T - 100 = 10 - T$ $2T = 110$ $T = 55^\circ C$.