Question
Question: If the difference between the roots of the equation $x^2 + ax + 1 = 0$ is less than $\sqrt{5}$, then...
If the difference between the roots of the equation x2+ax+1=0 is less than 5, then the set of possible values of a is
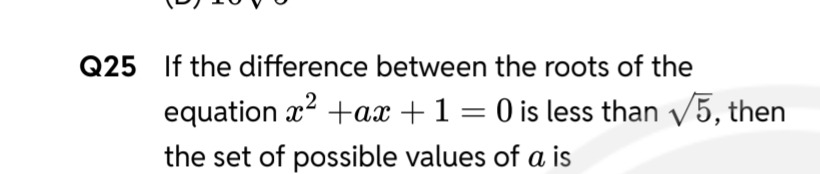
(-3, -2] ∪ [2, 3)
Solution
Let the roots of the quadratic equation x2+ax+1=0 be α and β. According to Vieta's formulas:
- Sum of the roots: α+β=−a
- Product of the roots: αβ=1
The difference between the roots, ∣α−β∣, can be expressed using the identity (α−β)2=(α+β)2−4αβ. Substituting the values from Vieta's formulas: (α−β)2=(−a)2−4(1) (α−β)2=a2−4
Therefore, ∣α−β∣=a2−4.
The problem states that the difference between the roots is less than 5: ∣α−β∣<5 Substitute the expression for ∣α−β∣: a2−4<5
To solve this inequality, we square both sides (both sides are non-negative): (a2−4)2<(5)2 a2−4<5 a2<9
This inequality implies −3<a<3.
Additionally, for the roots to be real (which is implicitly assumed when talking about their difference), the discriminant of the quadratic equation must be non-negative. The discriminant D for the equation Ax2+Bx+C=0 is D=B2−4AC. For x2+ax+1=0, A=1, B=a, C=1. So, D=a2−4(1)(1)=a2−4.
For real roots, D≥0: a2−4≥0 a2≥4
This inequality implies a≤−2 or a≥2.
Now, we need to find the values of a that satisfy both conditions:
- −3<a<3
- a≤−2 or a≥2
Let's visualize these conditions on a number line: Condition 1: a∈(−3,3) Condition 2: a∈(−∞,−2]∪[2,∞)
The intersection of these two sets is: (−3,−2]∪[2,3)
This means the possible values of a are such that −3<a≤−2 or 2≤a<3.
