Question
Question: Equivalent capacitance between A and B is nC. Write n ...
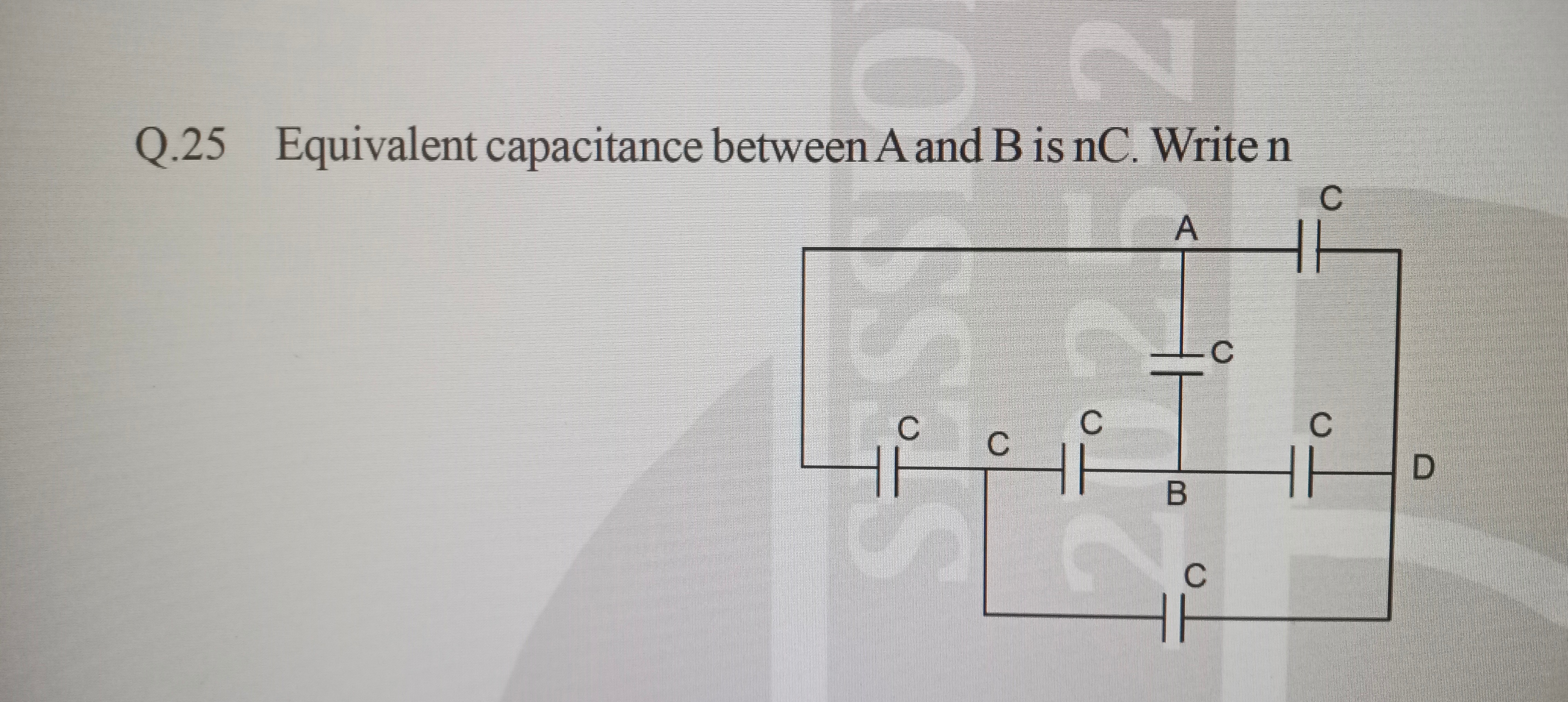
Equivalent capacitance between A and B is nC. Write n
1.625
Solution
To find the equivalent capacitance between A and B, we can simplify the circuit step-by-step.
-
Simplify the leftmost series branch:
The four capacitors on the left (A-Q, Q-P, P-Z, Z-B) are connected in series. Each has capacitance C.
The equivalent capacitance of these four capacitors in series is:
Cseries1=C1+C1+C1+C11=C41=4C -
Simplify the bottom-right series branch:
The two capacitors at the bottom (B-Y, Y-D) are connected in series. Each has capacitance C.
The equivalent capacitance of these two capacitors in series is:
Cseries2=C1+C11=C21=2C
This Cseries2 is connected between points B and D. -
Simplify the parallel combination between B and D:
The capacitor CBD (between B and D, with capacitance C) is in parallel with the equivalent capacitance Cseries2=C/2 (between B and D).
The equivalent capacitance between B and D is:
CBD,eff=CBD+Cseries2=C+2C=23C -
Redraw the simplified circuit:
Now, the circuit looks like this:- A direct capacitor CAB (vertical C) between A and B.
- The Cseries1=C/4 between A and B.
- A branch from A to X (C), then X to D (C), then D to B (with CBD,eff=3C/2).
This is a network of capacitors. The direct CAB and Cseries1 are in parallel, so their equivalent is C+C/4=5C/4.
Let's call the remaining part CAXDB. This part is connected in parallel with the 5C/4 equivalent.We need to find the equivalent capacitance of the A-X-D-B part. This is a three-capacitor network: CAX=C, CXD=C, CDB,eff=3C/2.
This is a simple series connection if we consider the path A-X-D-B. The equivalent capacitance for this path is:
CAXDB=CAX1+CXD1+CDB,eff11=C1+C1+3C/211=C1+C1+3C21
CAXDB=3C3+3+21=3C81=83CNow, all three parts are in parallel between A and B:
- The direct capacitor CAB=C.
- The series branch Cseries1=C/4.
- The series branch CAXDB=3C/8.
The total equivalent capacitance Ceq between A and B is the sum of these parallel capacitances:
Ceq=C+Cseries1+CAXDB
Ceq=C+4C+83C
To add these, find a common denominator, which is 8:
Ceq=88C+82C+83C
Ceq=8(8+2+3)C=813C
The problem states that the equivalent capacitance is nC.
Comparing 813C with nC, we get n=813.
The value of n is 813 or 1.625.
