Question
Question: A line meets the co-ordinate axes in A and B. A circle is circumscribed about the triangle OAB. If d...
A line meets the co-ordinate axes in A and B. A circle is circumscribed about the triangle OAB. If d₁ and d₂ are the distances of the tangent to the circle at the origin O from the points A and B respectively, the diameter of the circle is :
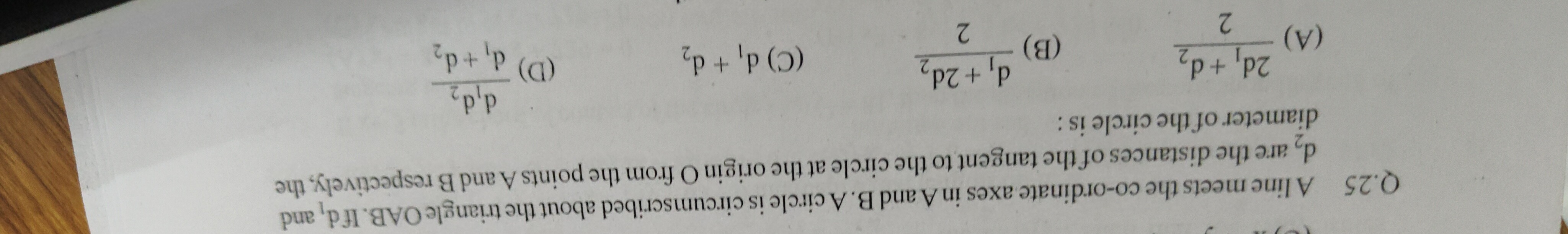
22d1+d2
2d1+2d2
d1+d2
d1+d2d1d2
d1+d2
Solution
Let the line meeting the co-ordinate axes at A and B be ax+by=1. Thus, the coordinates of A are (a,0) and the coordinates of B are (0,b). O is the origin (0,0). The triangle OAB is a right-angled triangle with the right angle at O. The circle circumscribed about △OAB has the hypotenuse AB as its diameter. The length of the diameter D is the distance between A and B: D=(a−0)2+(0−b)2=a2+b2. The equation of the circle circumscribing △OAB is x2−ax+y2−by=0. The tangent to the circle at the origin O(0,0) is ax+by=0. d1 is the distance of the tangent line ax+by=0 from point A(a,0): d1=a2+b2∣a(a)+b(0)+0∣=a2+b2a2. d2 is the distance of the tangent line ax+by=0 from point B(0,b): d2=a2+b2∣a(0)+b(b)+0∣=a2+b2b2. Summing d1 and d2: d1+d2=a2+b2a2+a2+b2b2=a2+b2a2+b2=a2+b2. Since D=a2+b2, we have D=d1+d2.
