Question
Question: The number of solution(s) of the equation $z^2=4z+|z|^2+$ $\frac{16}{|z|^3}$ is (where z=x+iy, x, y ...
The number of solution(s) of the equation z2=4z+∣z∣2+ ∣z∣316 is (where z=x+iy, x, y ∈ R, i2 = -1 and x ≠ 2)
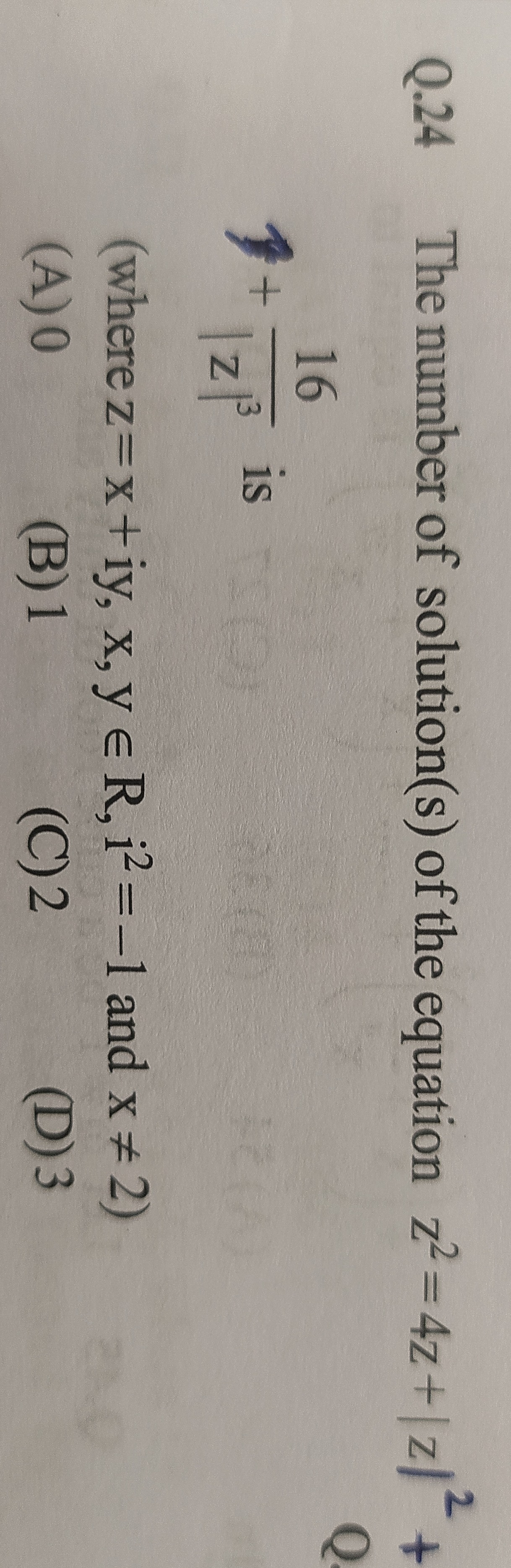
0
1
2
3
1
Solution
Solution:
Given the equation
z2=4z+∣z∣2+∣z∣316with z=reiθ (where r=∣z∣>0 and x=2), rewrite the equation as:
r2e2iθ=4reiθ+r2+r316.Dividing through by r (since r>0) we obtain
re2iθ=4eiθ+r+r416.Step 1. Equate the imaginary parts:
Write
e2iθ=cos2θ+isin2θ,eiθ=cosθ+isinθ.Then the imaginary part gives:
rsin2θ=4sinθ.Since sin2θ=2sinθcosθ, we have
2rsinθcosθ=4sinθ.There are two cases:
Case 1: sinθ=0 Dividing by sinθ:
2rcosθ=4⟹rcosθ=2.Substituting this into the real part (next step) will lead to a contradiction (a negative value for r5 that is impossible for r>0). Thus no solution arises from this case.
Case 2: sinθ=0 This implies θ=0 or θ=π.
Subcase 2a: θ=0 (so z=r, a positive real number) The equation becomes:
r2=4r+r2+r316.Cancel r2 from both sides:
0=4r+r316.Multiplying by r3:
0=4r4+16⟹4r4=−16,which is impossible for r>0.
Subcase 2b: θ=π (so z=−r) Now eiπ=−1 and e2iπ=1. The equation becomes:
r2=4(−r)+r2+r316.Cancelling r2 from both sides:
0=−4r+r316.Multiply by r3:
0=−4r4+16⟹4r4=16⟹r4=4.Hence,
r=44=41/4=2.This gives the unique solution:
z=−2.Conclusion: There is exactly 1 solution.
