Question
Question: The number of solution(s) of the equation $z^2=4z+|z|^2$ $\frac{16}{|z|^3}$ is (where $z=x+iy, x, y...
The number of solution(s) of the equation z2=4z+∣z∣2
∣z∣316 is (where z=x+iy,x,y∈R,i2=−1 and x=2)
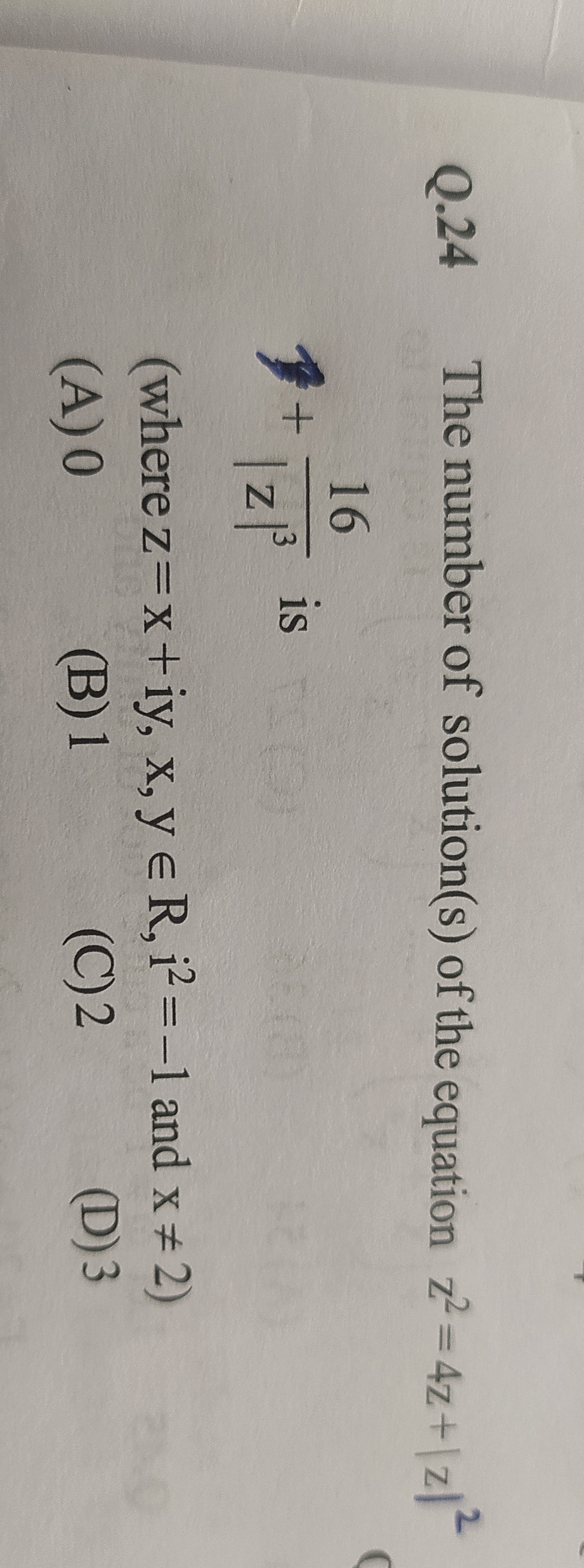
0
1
2
3
2
Solution
Solution:
We rewrite the given equation as
z2=4z+∣z∣2⋅∣z∣316=4z+∣z∣16,where z=reiθ and r=∣z∣>0.
Expressing in polar form:
z2=r2e2iθand4z=4reiθ.Thus the equation becomes
r2e2iθ=4reiθ+r16.Equate the imaginary parts:
r2sin2θ=4rsinθ.Using sin2θ=2sinθcosθ, we have
2r2sinθcosθ=4rsinθ.If sinθ=0, divide by sinθ (since sinθ is nonzero):
2r2cosθ=4r⟹rcosθ=2.Substituting this into the real part (where cos2θ=2cos2θ−1) eventually leads to a contradiction (since it would require r3 to be negative for positive r). Hence, we must have
sinθ=0.Thus, θ=0 or θ=π.
Case 1: θ=0
Here, z=r (a positive real). The equation becomes:
Multiplying by r (with r>0):
r3=4r2+16⟹r3−4r2−16=0.This cubic in r has exactly one positive root (by the Intermediate Value Theorem). Also, x=r=2 is maintained.
Case 2: θ=π
Here, z=−r (with r>0). Now:
Multiplying by r:
r3=−4r2+16⟹r3+4r2−16=0.This equation also has exactly one positive root.
Conclusion:
There are exactly 2 solutions corresponding to θ=0 and θ=π.
Minimal Explanation of the Solution:
Let z=reiθ. Equate imaginary parts; sinθ must be 0, so θ=0 or π. For each, the resulting real equation in r has one positive solution. Hence, the original equation has 2 solutions.
