Question

The number of solution(s) of the equation $z^2 = 4z + |z|$

$|2 + \frac{16}{|z|^3}|$ is

(where z=x+iy, x,y $\in$ R, $i^2 = -1$ and x $\neq$ 2)

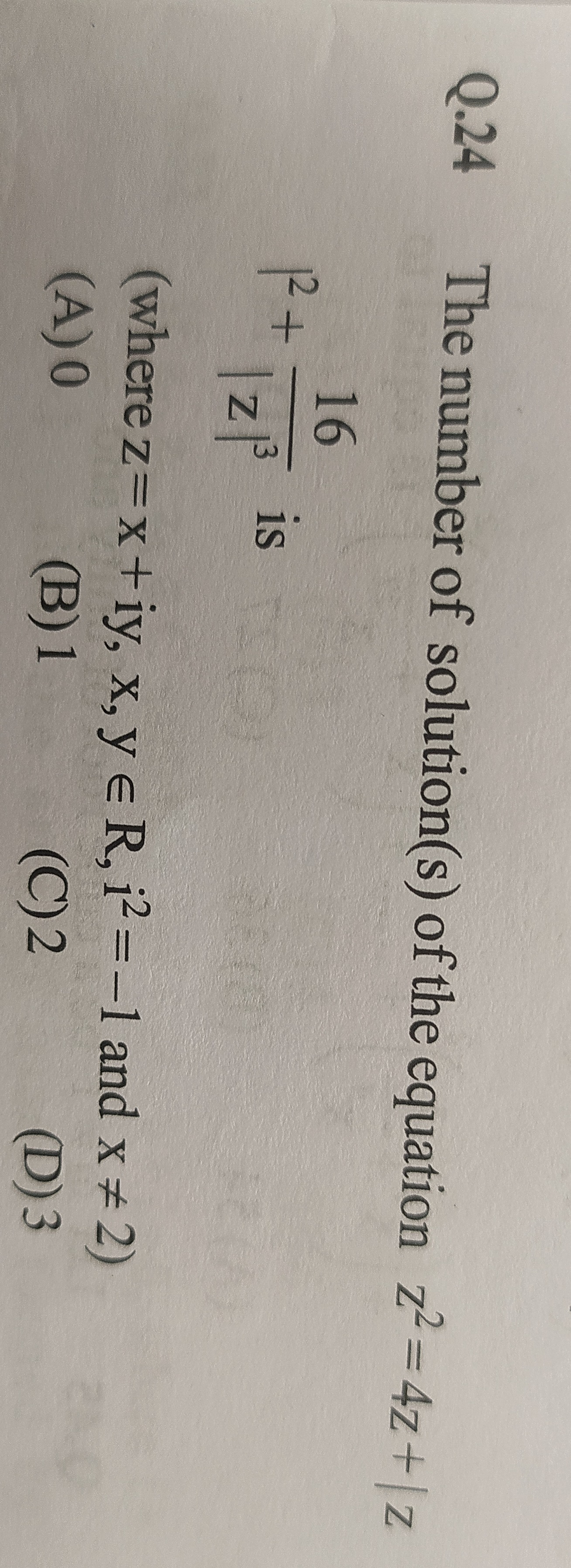
• A. 0
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (C)

2

Answer 2

We are to solve for complex numbers $z = re^{i\theta}$ (with $r = |z| > 0$) satisfying

$$z^2 = 4z + |z|\,\Bigl|2+\frac{16}{|z|^3}\Bigr|.$$

Since

$$\Bigl|2+\frac{16}{|z|^3}\Bigr| = 2+\frac{16}{r^3}\quad \text{(because } r>0 \text{)},$$

the equation becomes

$$z^2 = 4z + r\left(2+\frac{16}{r^3}\right).$$

Writing $z = re^{i\theta}$, note that

$$z^2 = r^2 e^{2i\theta} \quad \text{and} \quad 4z = 4re^{i\theta}.$$

Thus, dividing the entire equation by $r$ (since $r\neq 0$) we obtain

$$r e^{2i\theta} = 4e^{i\theta} + \left(2+\frac{16}{r^3}\right).$$

Write this in rectangular form:

$$r(\cos 2\theta + i\sin 2\theta) = 4(\cos\theta + i\sin\theta) + \left(2+\frac{16}{r^3}\right).$$

Equate the imaginary parts:

$$r\sin 2\theta = 4\sin\theta.$$

Since

$$\sin 2\theta = 2\sin\theta\cos\theta,$$

for $\sin\theta\neq 0$ we have

$$2r\sin\theta\cos\theta = 4\sin\theta \quad\Longrightarrow\quad r\cos\theta =2.$$

But then the real parts become (with $\cos2\theta= 2\cos^2\theta-1$):

$$r(2\cos^2\theta-1) = 4\cos\theta + \left(2+\frac{16}{r^3}\right).$$

Substituting $\cos\theta=\frac{2}{r}$ (from $r\cos\theta=2$) we get:

$$r\left(2\frac{4}{r^2}-1\right)=\frac{8}{r}+2+\frac{16}{r^3}.$$

Simplifying gives

$$\frac{8}{r}-r = \frac{8}{r}+2+\frac{16}{r^3},$$

or

$$-r = 2+\frac{16}{r^3}.$$

Multiplying by $r^3>0$ yields

$$-r^4 -2r^3 -16 = 0 \quad\Longrightarrow\quad r^4+2r^3+16 = 0,$$

which for $r>0$ has no solution. Hence, the only possibility is when

$$\sin\theta=0.$$

Thus, let $\theta=0$ or $\theta=\pi$.

Case 1: $\theta = 0$
Then $z = r$ (a positive real number). The equation becomes:

$$r e^{0} = 4 + \left(2+\frac{16}{r^3}\right) \quad\Longrightarrow\quad r = 6+\frac{16}{r^3}.$$

Multiplying by $r^3$ gives

$$r^4 - 6r^3 - 16 = 0.$$

For $r>0$ this equation has exactly one positive real root (found via the Intermediate Value Theorem), and $x\neq2$ is automatically satisfied since $r > 6$ approximately.

Case 2: $\theta = \pi$
Then $z = -r$ (with $r>0$). With $e^{2i\pi} = 1$ the equation becomes:

$$r = 4(-1) + \left(2+\frac{16}{r^3}\right) \quad\Longrightarrow\quad r = -4+2+\frac{16}{r^3},$$

or

$$r = -2 + \frac{16}{r^3}.$$

Rearrange:

$$r+2 = \frac{16}{r^3} \quad\Longrightarrow\quad r^4+2r^3-16 = 0.$$

Again, for $r>0$ this has exactly one positive real root (which can be shown through sign change analysis).

Thus, we obtain one valid solution for each of the angles $\theta=0$ and $\theta=\pi$.

Conclusion: There are 2 solutions.