Question

The determinant $\begin{vmatrix} x & a & a \\ a & x & a \\ a & a & x \end{vmatrix} =$

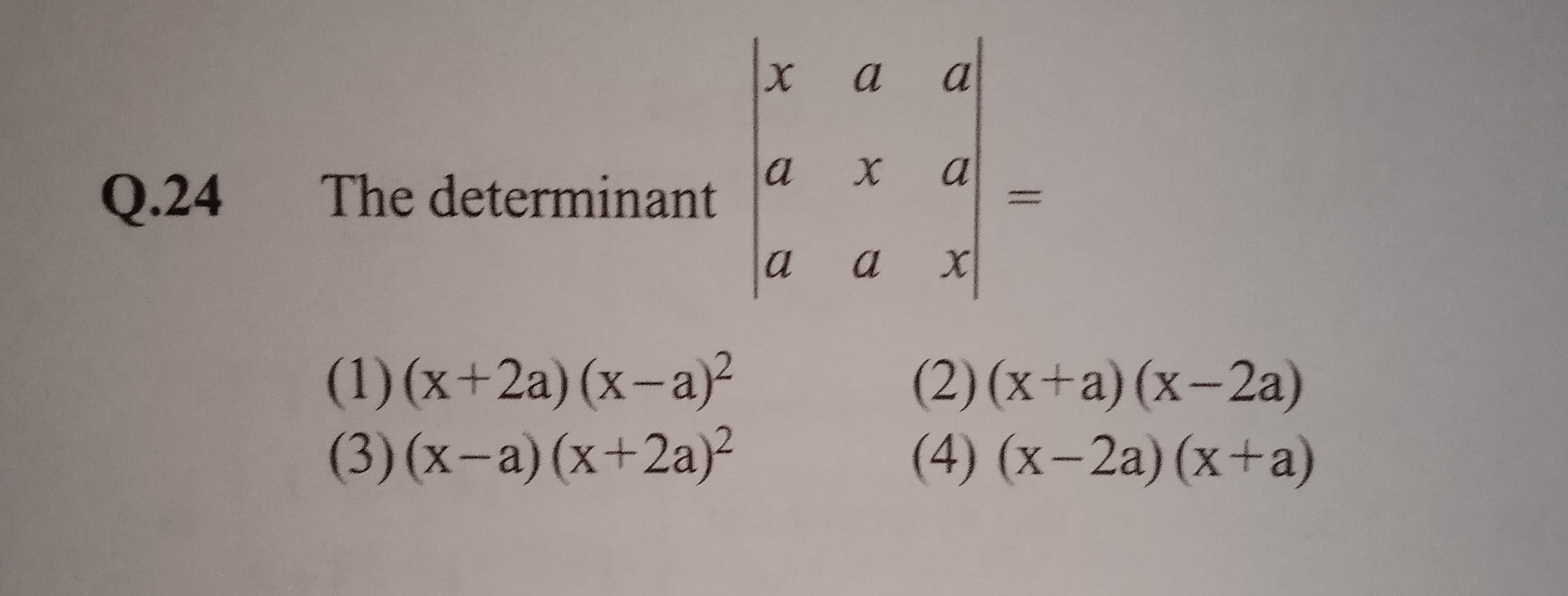
• A. $(x+2a)(x-a)^2$
• B. $(x+a)(x-2a)$
• C. $(x-a)(x+2a)^2$
• D. $(x-2a)(x+a)$

Answer 1

Answer: (A)

$(x+2a)(x-a)^2$

Answer 2

For the matrix

$$\begin{vmatrix} x & a & a \\ a & x & a \\ a & a & x \end{vmatrix},$$

a well-known formula for the determinant of a matrix with constant off-diagonal entries (and identical diagonal entries) is:

$$\det = (x-a)^2 (x+2a).$$

Thus, the correct option is (1) $(x+2a)(x-a)^2$.