Question
Question: Find area enclosed by $[|x|]+[|y|] = 2024$, [.]=GIF....
Find area enclosed by [∣x∣]+[∣y∣]=2024, [.]=GIF.
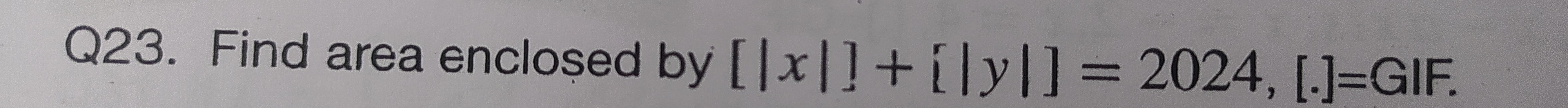
8100
Solution
The given equation is [∣x∣]+[∣y∣]=k, where k=2024. Here, [.] denotes the Greatest Integer Function (GIF).
Let Ix=[∣x∣] and Iy=[∣y∣]. Since Ix and Iy are results of the greatest integer function applied to non-negative values (∣x∣ and ∣y∣), Ix and Iy must be non-negative integers. So, we are looking for pairs of non-negative integers (Ix,Iy) such that Ix+Iy=k.
The possible pairs (Ix,Iy) are: (0,k),(1,k−1),(2,k−2),…,(k−1,1),(k,0). The number of such pairs is k+1.
For each pair (Ix,Iy), the equation defines a region in the xy-plane: Ix≤∣x∣<Ix+1 AND Iy≤∣y∣<Iy+1.
- For x:
- If Ix=0: 0≤∣x∣<1⟹−1<x<1. The length of this interval is 1−(−1)=2.
- If Ix>0: Ix≤∣x∣<Ix+1⟹(Ix≤x<Ix+1) or (−(Ix+1)<x≤−Ix). The length of the interval [Ix,Ix+1) is 1. The length of the interval (−(Ix+1),−Ix] is 1. The total length of the x-region is 1+1=2.
In both cases (Ix=0 or Ix>0), the total length of the x-region is 2.
- For y:
- Similarly, if Iy=0: 0≤∣y∣<1⟹−1<y<1. The length of this interval is 1−(−1)=2.
- If Iy>0: Iy≤∣y∣<Iy+1⟹(Iy≤y<Iy+1) or (−(Iy+1)<y≤−Iy). The length of the interval [Iy,Iy+1) is 1. The length of the interval (−(Iy+1),−Iy] is 1. The total length of the y-region is 1+1=2.
In both cases (Iy=0 or Iy>0), the total length of the y-region is 2.
For each pair (Ix,Iy), the region defined is a rectangle (or a union of rectangles) with dimensions 2 by 2. The area of each such region RIx,Iy is 2×2=4.
Since there are k+1 such disjoint regions, each with an area of 4, the total enclosed area is the sum of the areas of these regions. Total Area = (Number of pairs) × (Area of each region) = (k+1)×4=4k+4.
Substitute k=2024: Total Area = 4(2024)+4=8096+4=8100.
The area enclosed by [∣x∣]+[∣y∣]=2024 is 8100 square units.
