Solveeit Logo
Login

Question

Question: If C is a given non-zero scalar and $\overline{A}$ and $\overline{B}$ are given non-zero vectors suc...

If C is a given non-zero scalar and A‾\overline{A} and B‾\overline{B} are given non-zero vectors such that A‾\overline{A} is perpendicular to B‾\overline{B}. If vector X‾\overline{X} is such that A‾.X‾=C\overline{A}.\overline{X}=C and A‾×X‾=B‾\overline{A} \times \overline{X}=\overline{B} then X‾\overline{X} is given by

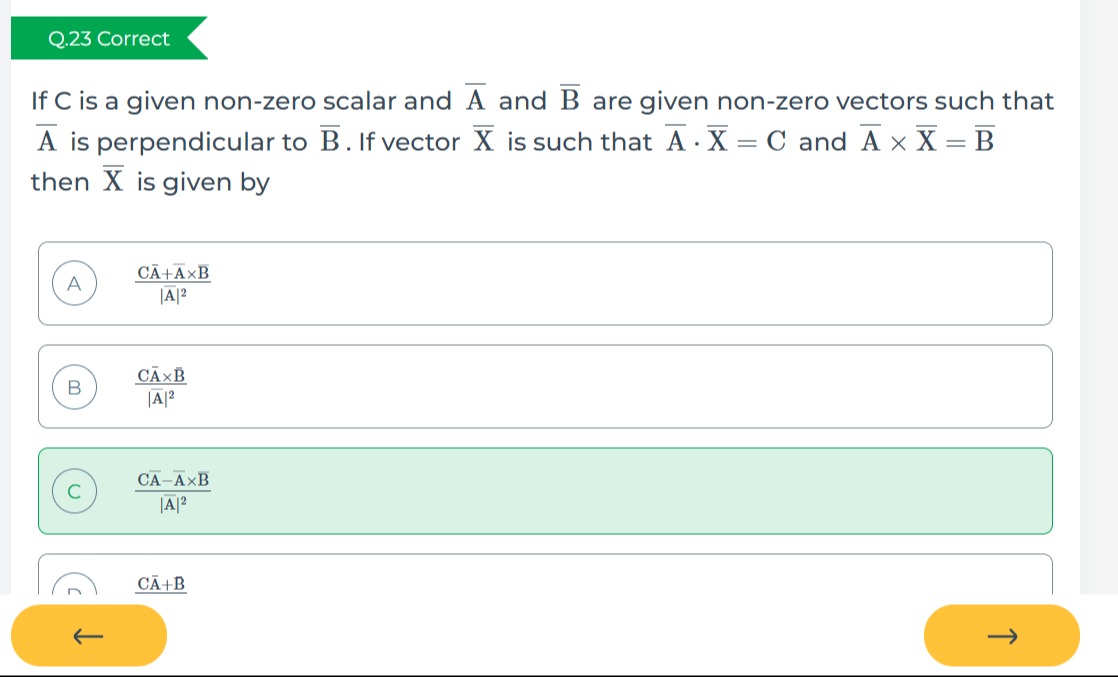
A

CA‾+A‾×B‾∣A‾∣2\frac{C\overline{A}+\overline{A}\times\overline{B}}{|\overline{A}|^2}

B

CA‾×B‾∣A‾∣2\frac{C\overline{A}\times\overline{B}}{|\overline{A}|^2}

C

CA‾−A‾×B‾∣A‾∣2\frac{C\overline{A}-\overline{A}\times\overline{B}}{|\overline{A}|^2}

D

CA‾+B‾\frac{C\overline{A}+\overline{B}}{}

Answer

Option C

Explanation

Solution

Solution Outline:

  1. We are given:

    • A⋅X=C\mathbf{A}\cdot \mathbf{X} = C
    • A×X=B\mathbf{A}\times \mathbf{X} = \mathbf{B}
    • A⊥B\mathbf{A} \perp \mathbf{B}

  2. Express X\mathbf{X} as:

    X=CA∣A∣2+Y\mathbf{X} = \frac{C\mathbf{A}}{|\mathbf{A}|^2} + \mathbf{Y}

    where Y\mathbf{Y} is a vector orthogonal to A\mathbf{A} (so that A⋅Y=0\mathbf{A}\cdot \mathbf{Y}=0).

  3. Substitute into the cross product:

    A×X=A×(CA∣A∣2+Y)=A×Y\mathbf{A}\times \mathbf{X} = \mathbf{A}\times \left(\frac{C\mathbf{A}}{|\mathbf{A}|^2} + \mathbf{Y}\right) = \mathbf{A}\times \mathbf{Y}

    because A×A=0\mathbf{A}\times \mathbf{A} = 0. We now require:

    A×Y=B\mathbf{A}\times \mathbf{Y} = \mathbf{B}

  4. A natural choice is to set:

    Y=−A×B∣A∣2\mathbf{Y} = -\frac{\mathbf{A}\times \mathbf{B}}{|\mathbf{A}|^2}

    so that:

    A×Y=−A×(A×B)∣A∣2\mathbf{A}\times \mathbf{Y} = -\frac{\mathbf{A}\times (\mathbf{A}\times \mathbf{B})}{|\mathbf{A}|^2}

    Using the vector triple product identity:

    A×(A×B)=A(A⋅B)−B∣A∣2=−B∣A∣2\mathbf{A}\times (\mathbf{A}\times \mathbf{B}) = \mathbf{A}(\mathbf{A}\cdot \mathbf{B}) - \mathbf{B}|\mathbf{A}|^2 = -\mathbf{B}|\mathbf{A}|^2

    (since A⋅B=0\mathbf{A}\cdot \mathbf{B}=0). Therefore:

    A×Y=−−B∣A∣2∣A∣2=B.\mathbf{A}\times \mathbf{Y} = -\frac{-\mathbf{B}|\mathbf{A}|^2}{|\mathbf{A}|^2} = \mathbf{B}.

  5. Thus, the required vector is:

    X=CA∣A∣2−A×B∣A∣2=CA−A×B∣A∣2\mathbf{X} = \frac{C\mathbf{A}}{|\mathbf{A}|^2} - \frac{\mathbf{A}\times \mathbf{B}}{|\mathbf{A}|^2} = \frac{C\mathbf{A} - \mathbf{A}\times \mathbf{B}}{|\mathbf{A}|^2}