Solveeit Logo
Login

Question

Question: A gas is taken through the cycle $A \rightarrow B \rightarrow C \rightarrow A$, as shown in the figu...

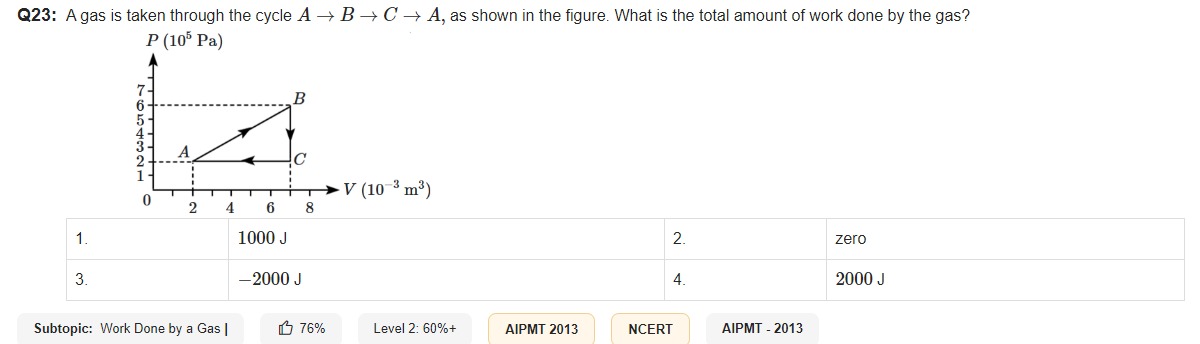
A gas is taken through the cycle A→B→C→AA \rightarrow B \rightarrow C \rightarrow A, as shown in the figure. What is the total amount of work done by the gas?

A

1000 J

B

zero

C

-2000 J

D

2000 J

Answer

1000 J

Explanation

Solution

The total work done by the gas in a cyclic process is the area enclosed by the cycle on the P-V diagram. The cycle forms a triangle with vertices A, B, and C. The coordinates are: A: VA=2×10−3 m3V_A = 2 \times 10^{-3} \text{ m}^3, PA=2×105 PaP_A = 2 \times 10^5 \text{ Pa} B: VB=7×10−3 m3V_B = 7 \times 10^{-3} \text{ m}^3, PB=6×105 PaP_B = 6 \times 10^5 \text{ Pa} C: VC=7×10−3 m3V_C = 7 \times 10^{-3} \text{ m}^3, PC=2×105 PaP_C = 2 \times 10^5 \text{ Pa}

The area of the triangle is: Area =12×(base)×(height)= \frac{1}{2} \times (\text{base}) \times (\text{height}) The base can be taken as the vertical distance PB−PC=(6×105−2×105) Pa=4×105 PaP_B - P_C = (6 \times 10^5 - 2 \times 10^5) \text{ Pa} = 4 \times 10^5 \text{ Pa}. The height is the horizontal distance VC−VA=(7×10−3−2×10−3) m3=5×10−3 m3V_C - V_A = (7 \times 10^{-3} - 2 \times 10^{-3}) \text{ m}^3 = 5 \times 10^{-3} \text{ m}^3. Area =12×(4×105 Pa)×(5×10−3 m3)=12×2000 J=1000 J= \frac{1}{2} \times (4 \times 10^5 \text{ Pa}) \times (5 \times 10^{-3} \text{ m}^3) = \frac{1}{2} \times 2000 \text{ J} = 1000 \text{ J}. Since the cycle A→B→C→AA \rightarrow B \rightarrow C \rightarrow A is traversed clockwise, the work done is positive.