Question
Question: A circle of constant radius 'a' passes through origin 'O' and cuts the axes of co-ordinates in point...
A circle of constant radius 'a' passes through origin 'O' and cuts the axes of co-ordinates in points P and Q, then the equation of the locus of the foot of perpendicular from O to PQ is:
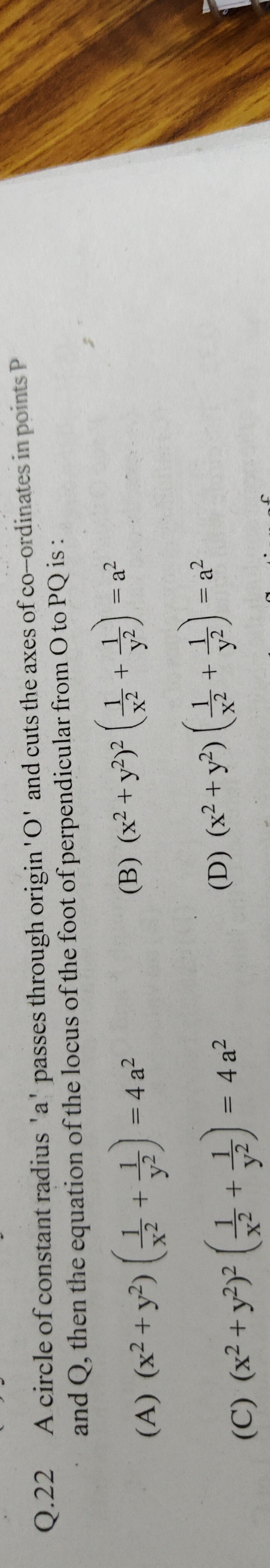
(x2+y2)2(x21+y21)=4a2
(x2+y2)2(x21+y21)=a2
(x2+y2)2(x21+y21)=4a2
(x2+y2)2(x21+y21)=a2
(x2+y2)2(x21+y21)=4a2
Solution
Let the equation of the circle be x2+y2+2gx+2fy=0 as it passes through the origin. The circle cuts the x-axis at P. Setting y=0, we get x2+2gx=0, so x(x+2g)=0. Thus, P=(−2g,0). The circle cuts the y-axis at Q. Setting x=0, we get y2+2fy=0, so y(y+2f)=0. Thus, Q=(0,−2f). The radius of the circle is given as 'a'. The radius of x2+y2+2gx+2fy+c=0 is g2+f2−c. Here c=0, so a=g2+f2, which means g2+f2=a2. The line PQ passes through P(−2g,0) and Q(0,−2f). The equation of line PQ is −2gx+−2fy=1, which simplifies to fx+gy+2fg=0. Let R(h, k) be the foot of the perpendicular from the origin O(0,0) to PQ. The slope of PQ is mPQ=0−(−2g)−2f−0=−gf. The slope of OR is mOR=hk. Since OR is perpendicular to PQ, mOR⋅mPQ=−1, so hk⋅(−gf)=−1, which gives kf=hg. The point R(h, k) also lies on the line PQ, so fh+gk+2fg=0. From kf=hg, we have g=hkf. Substituting this into fh+gk+2fg=0: fh+k(hkf)+2f(hkf)=0 fh2+k2f+2kf2=0 f(h2+k2+2kf)=0. This implies f=0 or h2+k2+2kf=0. If f=0, then g2=a2. From kf=hg, hg=0. If h=0, then k=0, giving R(h,0). If k=0, then h=0, giving R(0,k). If f=0, the line PQ is gx+2fg=0, which is gx=0 if g=0. This means x=0. The foot of the perpendicular from origin to x=0 is (0,0). If h2+k2+2kf=0, then f=−2kh2+k2. From kf=hg, g=hkf=hk(−2kh2+k2)=−2hh2+k2. Substitute these into g2+f2=a2: (−2hh2+k2)2+(−2kh2+k2)2=a2 4h2(h2+k2)2+4k2(h2+k2)2=a2 (h2+k2)2(4h21+4k21)=a2 (h2+k2)2(4h2k2k2+h2)=a2 4h2k2(h2+k2)3=a2 (h2+k2)3=4a2h2k2. Replacing (h,k) with (x,y): (x2+y2)3=4a2x2y2. Dividing by x2y2: x2y2(x2+y2)3=4a2. (x2+y2)2(x2y2x2+y2)=4a2. (x2+y2)2(y21+x21)=4a2.
