Question

$\int \frac{\sqrt{x^{2021}}}{1-x^{2023}}dx$

Answer 1

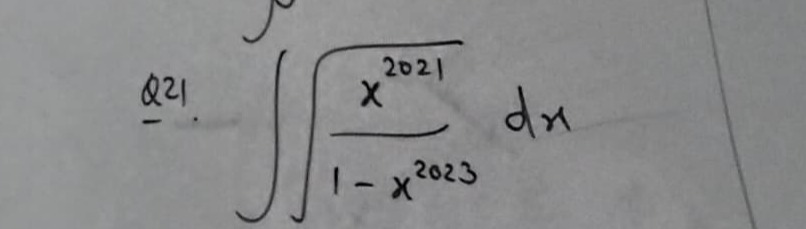
$\frac{1}{2023} \ln \left| \frac{1+x^{2023/2}}{1-x^{2023/2}} \right| + C$

Answer 2

To solve the integral $I = \int \frac{\sqrt{x^{2021}}}{1-x^{2023}}dx$, we use a substitution. Let $u = x^{2023}$. Then $du = 2023 x^{2022} dx$, which implies $dx = \frac{du}{2023 x^{2022}} = \frac{du}{2023 u^{2022/2023}}$. The numerator is $\sqrt{x^{2021}} = x^{2021/2}$. Since $x = u^{1/2023}$, we have $x^{2021/2} = (u^{1/2023})^{2021/2} = u^{2021/4046}$. Substituting these into the integral: $I = \int \frac{u^{2021/4046}}{1-u} \cdot \frac{du}{2023 u^{2022/2023}} = \frac{1}{2023} \int \frac{u^{2021/4046}}{1-u} u^{-2022/2023} du$. The exponent of $u$ simplifies to $\frac{2021}{4046} - \frac{2022}{2023} = \frac{2021 - 4044}{4046} = \frac{-2023}{4046} = -\frac{1}{2}$. So, $I = \frac{1}{2023} \int \frac{u^{-1/2}}{1-u} du$. Now, let $v = \sqrt{u}$. Then $u = v^2$ and $du = 2v dv$. $I = \frac{1}{2023} \int \frac{1}{v(1-v^2)} (2v dv) = \frac{2}{2023} \int \frac{1}{1-v^2} dv$. This is a standard integral: $\int \frac{1}{1-v^2} dv = \frac{1}{2} \ln \left| \frac{1+v}{1-v} \right| + C$. So, $I = \frac{2}{2023} \left( \frac{1}{2} \ln \left| \frac{1+v}{1-v} \right| \right) + C = \frac{1}{2023} \ln \left| \frac{1+v}{1-v} \right| + C$. Substituting back $v = \sqrt{u}$: $I = \frac{1}{2023} \ln \left| \frac{1+\sqrt{u}}{1-\sqrt{u}} \right| + C$. Finally, substituting back $u = x^{2023}$: $I = \frac{1}{2023} \ln \left| \frac{1+\sqrt{x^{2023}}}{1-\sqrt{x^{2023}}} \right| + C = \frac{1}{2023} \ln \left| \frac{1+x^{2023/2}}{1-x^{2023/2}} \right| + C$.