Question

Q.21. If $A = \begin{bmatrix} 1 & -1 & 2 \\ 0 & -1 & 3 \end{bmatrix}$, $B = \begin{bmatrix} -2 & 1 \\ 3 & -1 \\ 0 & 2 \end{bmatrix}$, show that AB is nonsingular.

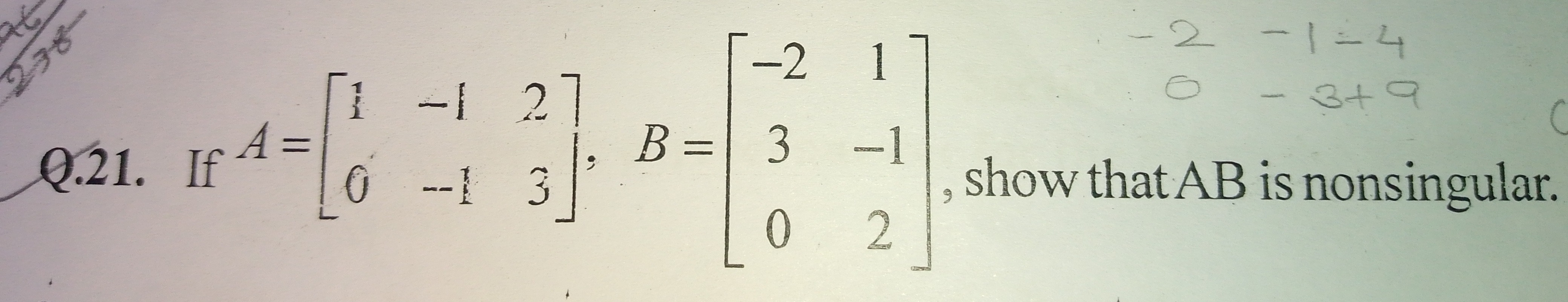
Answer 1

AB is nonsingular because its determinant is -17 ≠ 0.

Answer 2

We first compute the product $AB$. Given

$$A=\begin{bmatrix} 1 & -1 & 2 \\ 0 & -1 & 3 \end{bmatrix} \quad \text{and} \quad B=\begin{bmatrix} -2 & 1 \\ 3 & -1 \\ 0 & 2 \end{bmatrix},$$

the product $AB$ is a $2 \times 2$ matrix where:

• For the $(1,1)$ entry:
  $1\cdot(-2) + (-1)\cdot3 + 2\cdot0 = -2 - 3 = -5$.

• For the $(1,2)$ entry:
  $1\cdot1 + (-1)\cdot(-1) + 2\cdot2 = 1 + 1 + 4 = 6$.

• For the $(2,1)$ entry:
  $0\cdot(-2) + (-1)\cdot3 + 3\cdot0 = -3$.

• For the $(2,2)$ entry:
  $0\cdot1 + (-1)\cdot(-1) + 3\cdot2 = 1 + 6 = 7$.

Thus,

$$AB=\begin{bmatrix}-5 & 6 \\ -3 & 7 \end{bmatrix}.$$

To show that $AB$ is nonsingular, we calculate its determinant:

$$\det(AB)=(-5)(7)- (6)(-3) = -35 + 18 = -17.$$

Since $\det(AB) \neq 0$, the matrix $AB$ is nonsingular.