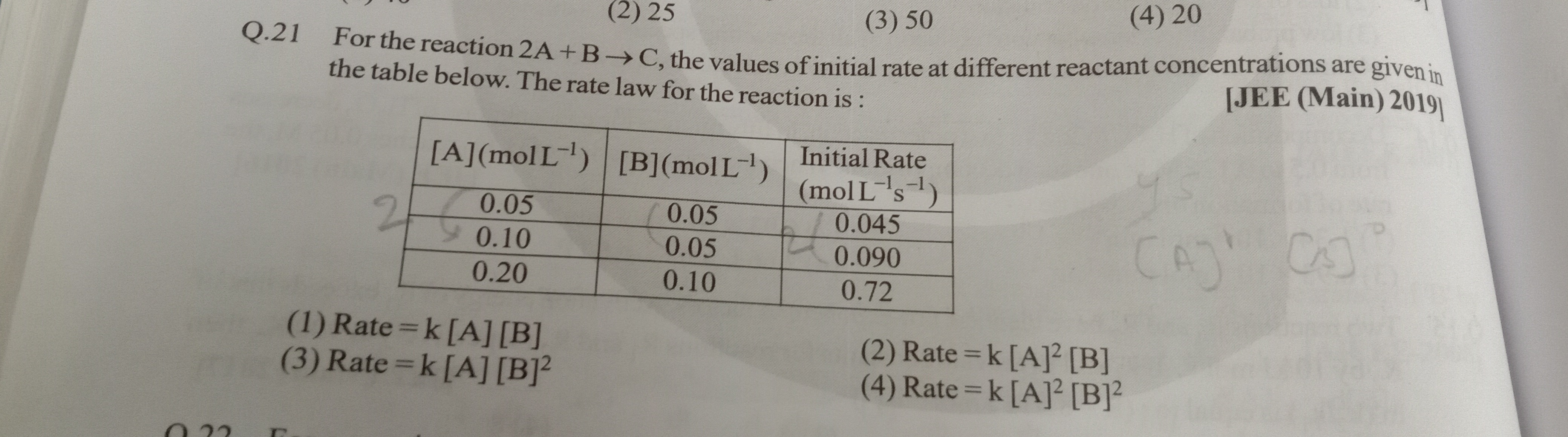Question

For the reaction 2A + B → C, the values of initial rate at different reactant concentrations are given in the table below. The rate law for the reaction is : [JEE (Main) 2019]

A	B	Initial Rate (mol L⁻¹s⁻¹)
0.05	0.05	0.045
0.10	0.05	0.090
0.20	0.10	0.72

• A. Rate = k [A] [B]
• B. Rate = k [A]² [B]
• C. Rate = k [A] [B]²
• D. Rate = k [A]² [B]²

Answer 1

Answer: (C)

Rate = k [A] [B]²

Answer 2

The rate law for a reaction of the form 2A + B → C is generally expressed as: Rate = k [A]^x [B]^y where x is the order of the reaction with respect to A, y is the order of the reaction with respect to B, and k is the rate constant. The values of x and y are determined experimentally.

We are given the following experimental data:

Experiment	A	B	Initial Rate (mol L⁻¹s⁻¹)
1	0.05	0.05	0.045
2	0.10	0.05	0.090
3	0.20	0.10	0.72

Step 1: Determine the order with respect to A (x). To find x, we compare experiments where the concentration of B remains constant. From Experiment 1 and Experiment 2, [B] is constant (0.05 molL⁻¹).

For Experiment 1: 0.045 = k (0.05)^x (0.05)^y (Equation 1)

For Experiment 2: 0.090 = k (0.10)^x (0.05)^y (Equation 2)

Divide Equation 2 by Equation 1: $\frac{0.090}{0.045} = \frac{k (0.10)^x (0.05)^y}{k (0.05)^x (0.05)^y}$ $2 = \left(\frac{0.10}{0.05}\right)^x$ $2 = (2)^x$ Therefore, x = 1. The reaction is first order with respect to A.

Step 2: Determine the order with respect to B (y). To find y, we can use Experiment 2 and Experiment 3, along with the value of x we just found.

For Experiment 2 (with x=1): 0.090 = k (0.10)^1 (0.05)^y (Equation 2')

For Experiment 3 (with x=1): 0.72 = k (0.20)^1 (0.10)^y (Equation 3)

Divide Equation 3 by Equation 2': $\frac{0.72}{0.090} = \frac{k (0.20)^1 (0.10)^y}{k (0.10)^1 (0.05)^y}$ $8 = \left(\frac{0.20}{0.10}\right)^1 \left(\frac{0.10}{0.05}\right)^y$ $8 = 2 \cdot (2)^y$ $\frac{8}{2} = (2)^y$ $4 = (2)^y$ Since 4 = 2^2, we have y = 2. The reaction is second order with respect to B.

Step 3: Write the complete rate law. Substitute the determined values of x and y into the general rate law expression: Rate = k [A]^1 [B]^2 Rate = k [A] [B]^2

The rate law for the reaction is Rate = k [A] [B]².

Explanation of the solution: The rate law is determined using the method of initial rates. By comparing experiments where one reactant's concentration is kept constant while the other's changes, the order with respect to each reactant can be found.

1. Comparing experiments 1 and 2 (where [B] is constant), doubling [A] doubles the rate, indicating Rate ∝ [A]^1. So, x = 1.
2. Comparing experiments 2 and 3 (using x=1), when [A] is doubled and [B] is doubled, the rate increases by a factor of 8. Since doubling [A] alone would double the rate (due to x=1), the remaining factor of 4 (8/2) must be due to the doubling of [B]. This implies Rate ∝ [B]^2. So, y = 2.
3. Combining these, the rate law is Rate = k [A] [B]^2.