Question

Find orthocentre of the triangle formed by the points $\left(ct_1,\frac{c}{t_1}\right)$, $\left(ct_2,\frac{c}{t_2}\right)$ and $\left(ct_3,\frac{c}{t_3}\right)$ and hence find circumcentre of the same triangle.

Answer 1

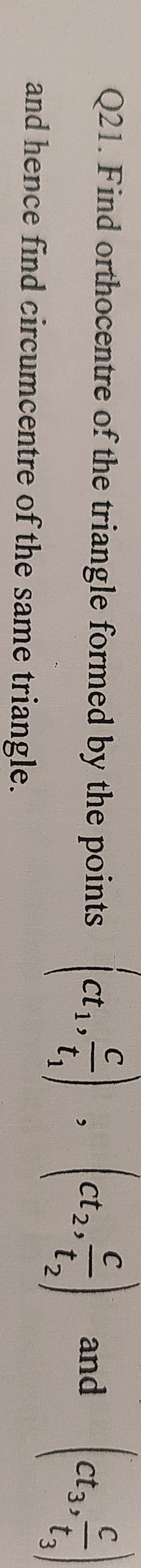
The orthocentre of the triangle is $\left(-\frac{c}{t_1 t_2 t_3}, -c t_1 t_2 t_3\right)$. The circumcentre of the triangle is $\left(\frac{c}{2}(t_1+t_2+t_3), \frac{c}{2}\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right)\right)$.

Answer 2

The vertices of the triangle are $A = \left(ct_1,\frac{c}{t_1}\right)$, $B = \left(ct_2,\frac{c}{t_2}\right)$, and $C = \left(ct_3,\frac{c}{t_3}\right)$. These points lie on the rectangular hyperbola $xy = c^2$.

1. Orthocentre: The slope of the side BC is $m_{BC} = -\frac{1}{t_2 t_3}$. The altitude from vertex A to BC has a slope $m_{AD} = t_2 t_3$. The equation of the altitude from A is $y - \frac{c}{t_1} = t_2 t_3 (x - ct_1)$, which simplifies to $y = t_2 t_3 x - c t_1 t_2 t_3 + \frac{c}{t_1}$ (1).

Similarly, the slope of the side AC is $m_{AC} = -\frac{1}{t_1 t_3}$. The altitude from vertex B to AC has a slope $m_{BE} = t_1 t_3$. The equation of the altitude from B is $y - \frac{c}{t_2} = t_1 t_3 (x - ct_2)$, which simplifies to $y = t_1 t_3 x - c t_1 t_2 t_3 + \frac{c}{t_2}$ (2).

Equating (1) and (2) to find the intersection (orthocentre H): $t_2 t_3 x - c t_1 t_2 t_3 + \frac{c}{t_1} = t_1 t_3 x - c t_1 t_2 t_3 + \frac{c}{t_2}$ $t_3 x (t_2 - t_1) = c \left(\frac{1}{t_2} - \frac{1}{t_1}\right) = c \frac{t_1 - t_2}{t_1 t_2}$ Assuming $t_1 \neq t_2$, we divide by $(t_2 - t_1)$: $t_3 x = - \frac{c}{t_1 t_2}$ $x = -\frac{c}{t_1 t_2 t_3}$

Substitute $x$ back into (1): $y = t_2 t_3 \left(-\frac{c}{t_1 t_2 t_3}\right) - c t_1 t_2 t_3 + \frac{c}{t_1}$ $y = -\frac{c}{t_1} - c t_1 t_2 t_3 + \frac{c}{t_1}$ $y = -c t_1 t_2 t_3$

The orthocentre $H$ is $\left(-\frac{c}{t_1 t_2 t_3}, -c t_1 t_2 t_3\right)$.

2. Circumcentre: For a triangle whose vertices lie on the rectangular hyperbola $xy=c^2$, the equation of the circumcircle is given by: $x^2 + y^2 - c(t_1+t_2+t_3)x - c\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right)y + c^2(t_1t_2+t_2t_3+t_3t_1) = 0$.

The general equation of a circle is $x^2 + y^2 + 2Gx + 2Fy + K = 0$. Comparing the two equations, we have: $2G = -c(t_1+t_2+t_3) \implies G = -\frac{c}{2}(t_1+t_2+t_3)$ $2F = -c\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right) \implies F = -\frac{c}{2}\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right)$

The circumcentre is $(-G, -F)$. Circumcentre $O = \left(\frac{c}{2}(t_1+t_2+t_3), \frac{c}{2}\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right)\right)$.