Question
Question: If $x^2 - 11x + a$ and $x^2 - 14x + 2a$ will have a common factor, then a =...
If x2−11x+a and x2−14x+2a will have a common factor, then a =
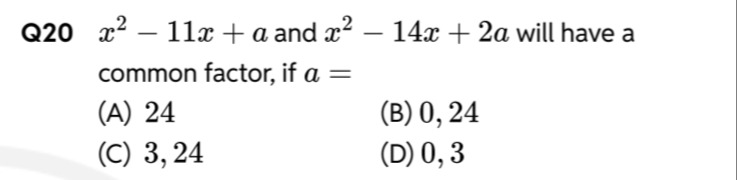
24
0, 24
3, 24
0, 3
0, 24
Solution
To find the values of 'a' for which the two quadratic expressions x2−11x+a and x2−14x+2a have a common factor, we can assume they share a common root, say α. If α is a common root, it must satisfy both equations:
- α2−11α+a=0
- α2−14α+2a=0
Subtract equation (1) from equation (2): (α2−14α+2a)−(α2−11α+a)=0 α2−14α+2a−α2+11α−a=0 −3α+a=0
This gives us a relationship between a and α: a=3α
Now substitute a=3α into equation (1): α2−11α+(3α)=0 α2−8α=0
Factor out α: α(α−8)=0
This equation yields two possible values for α:
Case 1: α=0 Case 2: α=8
Now, we find the corresponding values of 'a' using a=3α:
Case 1: If α=0 a=3×0 a=0
Case 2: If α=8 a=3×8 a=24
Thus, the values of 'a' for which the two expressions have a common factor are 0 and 24.
