Question
Question: $x^2 + x + 1 + 2k(x^2 - x - 1) = 0$ is a perfect square for how many values of $k$ ...
x2+x+1+2k(x2−x−1)=0 is a perfect square for how many values of k
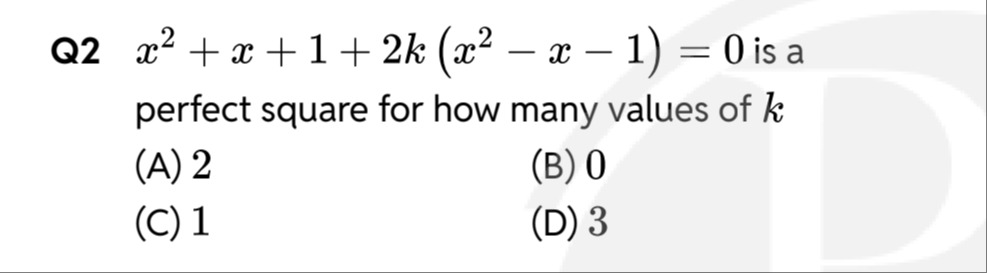
2
0
1
3
2
Solution
The problem asks for the number of values of k for which the given equation x2+x+1+2k(x2−x−1)=0 is a perfect square.
1. Rewrite the equation in standard quadratic form:
First, expand and rearrange the given equation into the standard quadratic form Ax2+Bx+C=0:
x2+x+1+2kx2−2kx−2k=0
Group terms by powers of x:
(1+2k)x2+(1−2k)x+(1−2k)=0
Comparing this with Ax2+Bx+C=0, we identify the coefficients:
A=1+2k B=1−2k C=1−2k
2. Apply the condition for a perfect square:
For a quadratic equation to be a perfect square (i.e., have equal roots), its discriminant (D) must be zero. The discriminant is given by the formula D=B2−4AC.
Set the discriminant to zero:
B2−4AC=0
Substitute the expressions for A, B, and C:
(1−2k)2−4(1+2k)(1−2k)=0
3. Solve for k:
Notice that (1−2k) is a common factor in both terms. Factor it out:
(1−2k)[(1−2k)−4(1+2k)]=0
This equation holds true if either of the factors is zero.
Case 1: The first factor is zero
1−2k=0 2k=1 k=21
Case 2: The second factor is zero
(1−2k)−4(1+2k)=0 1−2k−4−8k=0
Combine like terms:
(1−4)+(−2k−8k)=0 −3−10k=0 10k=−3 k=−103
4. Count the number of values of k:
We found two distinct values for k: k=21 and k=−103.
Therefore, there are 2 values of k for which the given equation is a perfect square.
