Question
Question: Write the duals of each of the following. i) $p \vee (q \wedge r)$ ii) $p \wedge (q \wedge r)$ iii)...
Write the duals of each of the following.
i) p∨(q∧r) ii) p∧(q∧r) iii) (p∨q)∧(r∨s) iv) p∧∼q v) (∼p∨q)∧(∼r∧s) vi) ∼p∧(∼q∧(p∨q)∧∼r) vii) [∼(s∼∨b)∼∧d]∨[(b∧d)∼] viii) c∨{p∧(q∨r)} ix) ∼p∨(q∧r)∧d∼(xi{(r∧b)∨d}∧c x) ∃∧(b∧d)(x⊥∨(r∨b)∧d∼
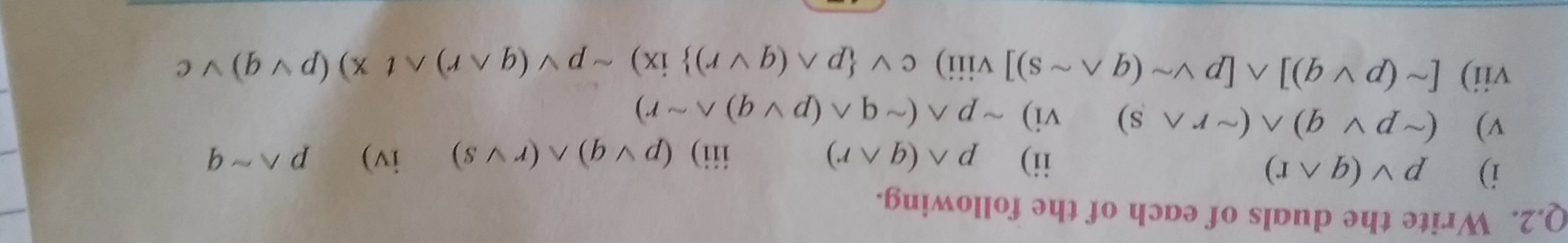
Answer
The dual of a Boolean expression is formed by interchanging every ∨ (OR) with ∧ (AND), and every ∧ (AND) with ∨ (OR), leaving the variables and complementation unchanged. Parts (ix) and (x) of the original question are unclear and cannot be solved.
Explanation
Solution
To find the dual of a Boolean expression, follow these steps:
- Identify all occurrences of the logical OR operator (∨) and the logical AND operator (∧).
- Replace each ∨ with ∧.
- Replace each ∧ with ∨.
- Leave all variables (e.g., p, q, r) and complements (¬p, ~q) unchanged.
For example, the dual of p∨(q∧r) is p∧(q∨r). This process effectively swaps the roles of conjunction and disjunction in the expression.
