Question

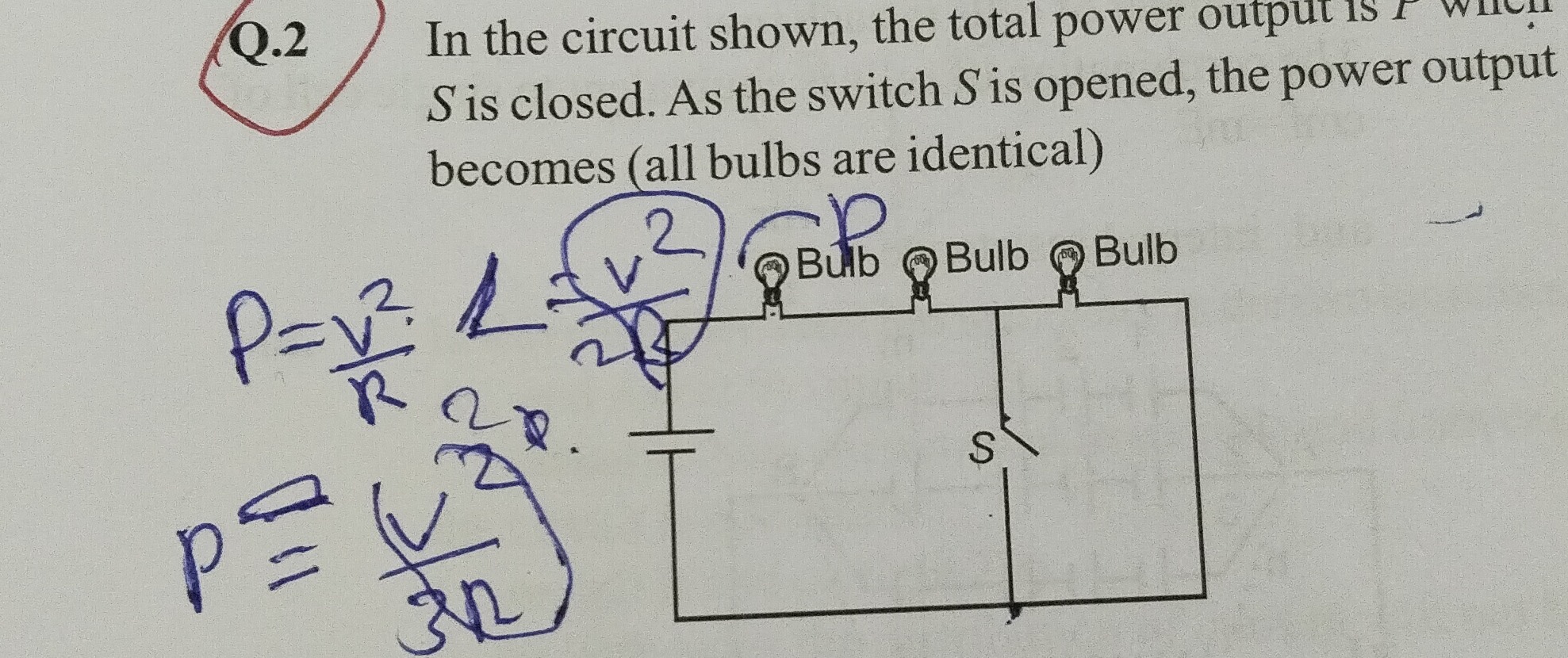
In the circuit shown, the total power output is P when S is closed. As the switch S is opened, the power output becomes (all bulbs are identical)

• A. P/3
• B. 2P/3
• C. P/2
• D. 3P/2

Answer 1

Answer: (B)

The power output becomes $\frac{2P}{3}$.

Answer 2

Let V be the voltage of the battery and R be the resistance of each identical bulb.

1. When switch S is closed: The circuit consists of three bulbs connected in series. The switch S is connected between the junction of the second and third bulb and the negative terminal of the battery. When closed, the switch offers negligible resistance, effectively short-circuiting the third bulb. Therefore, the circuit behaves as if only the first two bulbs are connected in series to the battery. The equivalent resistance is $R_{eq, closed} = R + R = 2R$. The total power output is given as P. Using the formula for power $P = \frac{V^2}{R_{eq}}$, we have: $P = \frac{V^2}{2R}$

2. When switch S is opened: When the switch S is opened, the short circuit is removed. The circuit now consists of all three bulbs connected in series to the battery. The equivalent resistance is $R_{eq, opened} = R + R + R = 3R$. The new power output, let's call it $P'$, is: $P' = \frac{V^2}{R_{eq, opened}} = \frac{V^2}{3R}$

3. Expressing the new power in terms of P: We are given $P = \frac{V^2}{2R}$. From this, we can express $\frac{V^2}{R}$ as $2P$. Now, substitute this into the expression for $P'$: $P' = \frac{1}{3} \left(\frac{V^2}{R}\right) = \frac{1}{3} (2P) = \frac{2P}{3}$

Thus, when the switch S is opened, the power output becomes $\frac{2P}{3}$.