Question
Question: If $f(x) = tan^{-1}x + \ln x$ then find $\frac{dy}{dx} @ x = \frac{\pi}{4}$ where $y = f^{-1}(x)$....
If f(x)=tan−1x+lnx then find dxdy@x=4π where y=f−1(x).
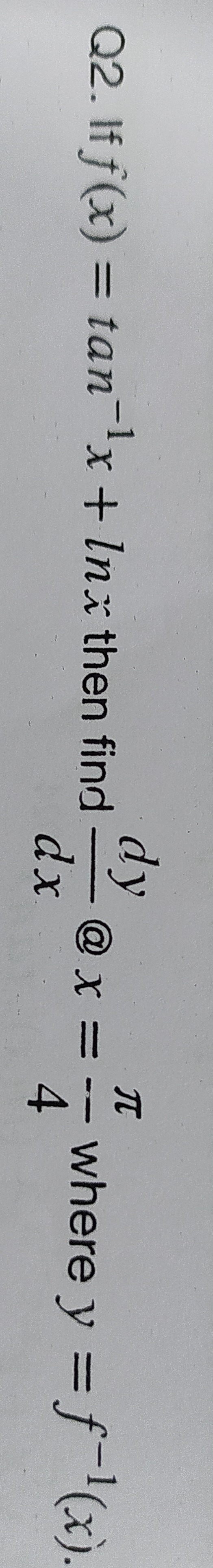
32
Solution
The problem asks us to find the derivative of the inverse function y=f−1(x) at a specific point x=4π, given the function f(x)=tan−1x+lnx.
-
Understand the relationship between a function and its inverse: If y=f−1(x), it means x=f(y).
-
Apply the inverse function differentiation rule: Differentiating x=f(y) with respect to x using the chain rule: dxd(x)=dxd(f(y))
1=f′(y)dxdy
Therefore, dxdy=f′(y)1.
-
Find the derivative of the original function f(x): Given f(x)=tan−1x+lnx. Differentiate f(x) with respect to x: f′(x)=dxd(tan−1x)+dxd(lnx)
f′(x)=1+x21+x1
-
Find the corresponding value of y for the given x value: We need to find dxdy at x=4π. This means we need to find the value of y such that f(y)=4π. Substitute y into f(x): f(y)=tan−1y+lny Set f(y)=4π: tan−1y+lny=4π By inspection, if we let y=1: tan−1(1)+ln(1)=4π+0=4π. So, when x=4π, the corresponding value of y is 1.
-
Evaluate f′(y) at the found y value: Substitute y=1 into the expression for f′(y): f′(1)=1+121+11
f′(1)=21+1
f′(1)=23
-
Calculate dxdy: Using the inverse function differentiation rule: dxdyx=4π=f′(1)1=231=32.
