Question
Question: If $C = \{x \in \mathbb{R} : |x+1| \leq 3\}$ and $D = \{x \in \mathbb{R} : |x-1| > 2\}$, then which ...
If C={x∈R:∣x+1∣≤3} and D={x∈R:∣x−1∣>2}, then which of the following is true?
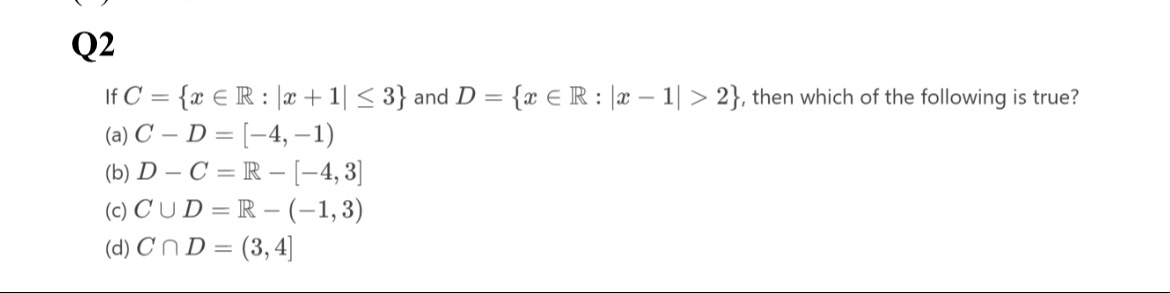
C−D=[−4,−1)
D−C=R−[−4,3]
C∪D=R−(−1,3)
C∩D=(3,4]
(b)
Solution
First, determine the interval representation of set C. The inequality ∣x+1∣≤3 is equivalent to −3≤x+1≤3. Subtracting 1 from all parts, we get −3−1≤x≤3−1, which simplifies to −4≤x≤2. So, C=[−4,2].
Next, determine the interval representation of set D. The inequality ∣x−1∣>2 is equivalent to x−1>2 or x−1<−2.
Case 1: x−1>2⟹x>2+1⟹x>3. Case 2: x−1<−2⟹x<−2+1⟹x<−1. So, D=(−∞,−1)∪(3,∞).
Now, let's evaluate each option.
(a) C−D=[−4,−1) C−D is the set of elements in C but not in D. C−D=[−4,2]∖((−∞,−1)∪(3,∞)). This is equivalent to the intersection of C with the complement of D. The complement of D, Dc, is R∖((−∞,−1)∪(3,∞))=[−1,3]. So, C−D=C∩Dc=[−4,2]∩[−1,3]. The intersection of [−4,2] and [−1,3] is [−1,2]. Thus, C−D=[−1,2]. Option (a) states C−D=[−4,−1), which is incorrect.
(b) D−C=R−[−4,3] D−C is the set of elements in D but not in C. D−C=((−∞,−1)∪(3,∞))∖[−4,2]. This is equivalent to the intersection of D with the complement of C. The complement of C, Cc, is R∖[−4,2]=(−∞,−4)∪(2,∞). So, D−C=D∩Cc=((−∞,−1)∪(3,∞))∩((−∞,−4)∪(2,∞)). We can find the intersection by distributing: D−C=((−∞,−1)∩(−∞,−4))∪((−∞,−1)∩(2,∞))∪((3,∞)∩(−∞,−4))∪((3,∞)∩(2,∞)).
(−∞,−1)∩(−∞,−4)=(−∞,−4). (−∞,−1)∩(2,∞)=∅. (3,∞)∩(−∞,−4)=∅. (3,∞)∩(2,∞)=(3,∞).
So, D−C=(−∞,−4)∪∅∪∅∪(3,∞)=(−∞,−4)∪(3,∞).
Now let's evaluate the right side of option (b): R−[−4,3]. R−[−4,3] is the set of all real numbers excluding the closed interval [−4,3]. This means x<−4 or x>3. So, R−[−4,3]=(−∞,−4)∪(3,∞). Comparing D−C=(−∞,−4)∪(3,∞) with R−[−4,3]=(−∞,−4)∪(3,∞), we see that they are equal. Thus, option (b) is true.
(c) C∪D=R−(−1,3) C∪D=[−4,2]∪((−∞,−1)∪(3,∞)). Combining the intervals: (−∞,−1)∪[−4,2]=(−∞,2]. So, C∪D=(−∞,2]∪(3,∞). The right side of option (c) is R−(−1,3), which is the set of all real numbers excluding the open interval (−1,3). This means x≤−1 or x≥3. So, R−(−1,3)=(−∞,−1]∪[3,∞). Comparing C∪D=(−∞,2]∪(3,∞) with R−(−1,3)=(−∞,−1]∪[3,∞), we see that they are not equal. For example, x=0 is in C∪D but not in R−(−1,3). Option (c) is incorrect.
(d) C∩D=(3,4] C∩D=[−4,2]∩((−∞,−1)∪(3,∞)). C∩D=([−4,2]∩(−∞,−1))∪([−4,2]∩(3,∞)). [−4,2]∩(−∞,−1)=[−4,−1). [−4,2]∩(3,∞)=∅. So, C∩D=[−4,−1)∪∅=[−4,−1). Option (d) states C∩D=(3,4], which is incorrect.
Based on the evaluation of all options, only option (b) is true.
