Question

If $a_1, a_2 ... a_{10}$ are positive real numbers such that $(a_1.a_2.a_3 ... a_{10}) = 512$ then find the min value of $a_1 + a_2 + ... + a_9 + 2a_{10}$.

Answer 1

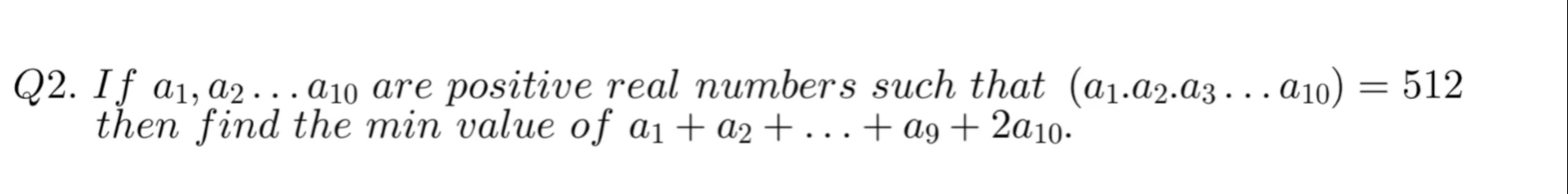
20

Answer 2

The problem asks for the minimum value of $a_1 + a_2 + ... + a_9 + 2a_{10}$, given that $a_1, a_2, ..., a_{10}$ are positive real numbers and their product $(a_1.a_2.a_3 ... a_{10}) = 512$.

We can use the AM-GM (Arithmetic Mean - Geometric Mean) inequality. For a set of $n$ positive real numbers $x_1, x_2, ..., x_n$, the AM-GM inequality states:

$\frac{x_1 + x_2 + ... + x_n}{n} \ge (x_1 x_2 ... x_n)^{1/n}$

Equality holds when $x_1 = x_2 = ... = x_n$.

In this problem, we want to find the minimum value of the sum $S = a_1 + a_2 + ... + a_9 + 2a_{10}$. Let's consider these 10 terms as $x_1 = a_1, x_2 = a_2, ..., x_9 = a_9, x_{10} = 2a_{10}$.

Now, apply the AM-GM inequality to these 10 terms:

$\frac{a_1 + a_2 + ... + a_9 + 2a_{10}}{10} \ge (a_1 \cdot a_2 \cdot ... \cdot a_9 \cdot (2a_{10}))^{1/10}$

Let's evaluate the product term inside the parenthesis:

$P' = a_1 \cdot a_2 \cdot ... \cdot a_9 \cdot (2a_{10})$

We can rewrite this product as:

$P' = 2 \cdot (a_1 \cdot a_2 \cdot ... \cdot a_9 \cdot a_{10})$

We are given that $a_1 \cdot a_2 \cdot ... \cdot a_{10} = 512$. Substitute this value into the product $P'$:

$P' = 2 \cdot 512 = 1024$

Now, substitute $P'$ back into the AM-GM inequality:

$\frac{a_1 + a_2 + ... + a_9 + 2a_{10}}{10} \ge (1024)^{1/10}$

We know that $1024 = 2^{10}$. So, $(1024)^{1/10} = (2^{10})^{1/10} = 2$.

$\frac{a_1 + a_2 + ... + a_9 + 2a_{10}}{10} \ge 2$

Multiply both sides by 10:

$a_1 + a_2 + ... + a_9 + 2a_{10} \ge 20$

The minimum value of the expression is 20. The equality holds when all the terms in the AM-GM inequality are equal: $a_1 = a_2 = ... = a_9 = 2a_{10}$. Let $a_1 = k$. Then $a_1 = a_2 = ... = a_9 = k$ and $2a_{10} = k$, which implies $a_{10} = k/2$. Substitute these values into the product condition: $a_1 \cdot a_2 \cdot ... \cdot a_9 \cdot a_{10} = 512$ $k^9 \cdot (k/2) = 512$ $k^{10}/2 = 512$ $k^{10} = 1024$ $k = (1024)^{1/10} = 2$.

So, the values for which the minimum occurs are: $a_1 = a_2 = ... = a_9 = 2$ $a_{10} = k/2 = 2/2 = 1$.

Let's verify the sum with these values: $a_1 + ... + a_9 + 2a_{10} = (9 \times 2) + (2 \times 1) = 18 + 2 = 20$. This confirms that the minimum value is indeed 20.