Solveeit Logo
Login

Question

Question: If $(a-b)x^2 + (b-c)x + (c-a) = 0$ then roots of this eqⁿ will be...

If (a−b)x2+(b−c)x+(c−a)=0(a-b)x^2 + (b-c)x + (c-a) = 0 then roots of this eqⁿ will be

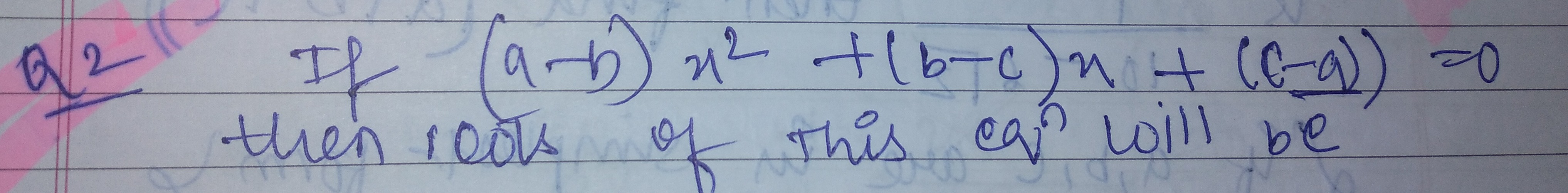
A

1 and a−bc−a\frac{a-b}{c-a}

B

1 and c−aa−b\frac{c-a}{a-b}

C

1 and b−ca−b\frac{b-c}{a-b}

D

1 and a−cb−a\frac{a-c}{b-a}

Answer

1 and c−aa−b\frac{c-a}{a-b}

Explanation

Solution

The sum of the coefficients of the quadratic equation (a−b)x2+(b−c)x+(c−a)=0(a-b)x^2 + (b-c)x + (c-a) = 0 is (a−b)+(b−c)+(c−a)=0(a-b) + (b-c) + (c-a) = 0. This implies that x=1x=1 is a root. For a quadratic equation Ax2+Bx+C=0Ax^2+Bx+C=0, the product of roots is C/AC/A. With one root being 11, the other root is found to be c−aa−b\frac{c-a}{a-b}.