Question

Let a, b, c be positive numbers. The following system of equations in x, y & z:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 ; \frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 ; -\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

has:

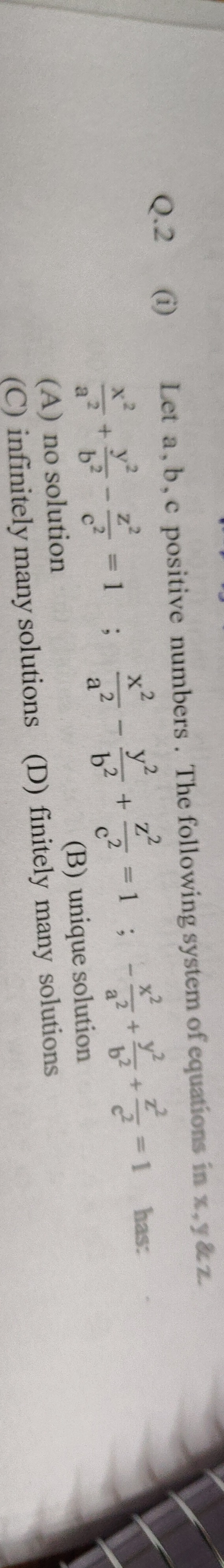
• A. no solution
• B. unique solution
• C. infinitely many solutions
• D. finitely many solutions

Answer 1

Answer: (D)

finitely many solutions

Answer 2

The given system of equations is:

1. $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$
2. $\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
3. $-\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

Let's simplify the system by introducing new variables. Let $X = \frac{x^2}{a^2}$, $Y = \frac{y^2}{b^2}$, and $Z = \frac{z^2}{c^2}$. Since $a, b, c$ are positive numbers, $a^2, b^2, c^2$ are positive. Also, $x^2, y^2, z^2$ must be non-negative for real solutions. Therefore, $X \ge 0$, $Y \ge 0$, $Z \ge 0$.

The system of equations transforms into a linear system in terms of X, Y, Z: I) $X + Y - Z = 1$ II) $X - Y + Z = 1$ III) $-X + Y + Z = 1$

Now, we solve this linear system:

1. Add equation (I) and equation (II): $(X + Y - Z) + (X - Y + Z) = 1 + 1$ $2X = 2$ $X = 1$

2. Add equation (I) and equation (III): $(X + Y - Z) + (-X + Y + Z) = 1 + 1$ $2Y = 2$ $Y = 1$

3. Add equation (II) and equation (III): $(X - Y + Z) + (-X + Y + Z) = 1 + 1$ $2Z = 2$ $Z = 1$

So, the unique solution for $(X, Y, Z)$ is $(1, 1, 1)$. These values satisfy the non-negativity conditions ($X=1 \ge 0$, $Y=1 \ge 0$, $Z=1 \ge 0$).

Now, substitute back the original expressions for X, Y, Z:

• For X: $\frac{x^2}{a^2} = 1 \implies x^2 = a^2 \implies x = \pm a$

• For Y: $\frac{y^2}{b^2} = 1 \implies y^2 = b^2 \implies y = \pm b$

• For Z: $\frac{z^2}{c^2} = 1 \implies z^2 = c^2 \implies z = \pm c$

Since $a, b, c$ are positive numbers, $a \ne 0$, $b \ne 0$, $c \ne 0$. This means that $x=\pm a$ gives two distinct values ($a$ and $-a$), similarly for $y$ and $z$.

The possible values for $(x, y, z)$ are:

• $x$ can be $a$ or $-a$ (2 choices)
• $y$ can be $b$ or $-b$ (2 choices)
• $z$ can be $c$ or $-c$ (2 choices)

Since the choices for $x$, $y$, and $z$ are independent, the total number of distinct solutions $(x, y, z)$ is $2 \times 2 \times 2 = 8$.

These 8 solutions are: $(a, b, c)$, $(a, b, -c)$, $(a, -b, c)$, $(a, -b, -c)$, $(-a, b, c)$, $(-a, b, -c)$, $(-a, -b, c)$, $(-a, -b, -c)$.

Since the number of solutions is 8, which is a finite number, the system has finitely many solutions.