Question

Find positive numbers, $x$, $y$ and $z$ such that
$x + 2y + 3z = 9$
and
$x^3 + 8y^3 + 27z^3 = 18\,x\,y\,z.$

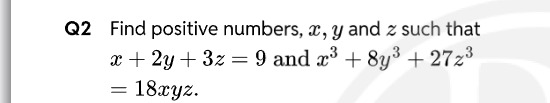
Answer 1

$(x,y,z) = \bigl(3,\tfrac{3}{2},1\bigr)$

Answer 2

Solution Outline

1. Set $$a = x,\quad b = 2y,\quad c = 3z.$$ Then the first equation becomes $$a + b + c = 9.$$
2. Note that $$x^3 + 8y^3 + 27z^3 = a^3 + b^3 + c^3,$$ and $$xyz = a\cdot\frac{b}{2}\cdot\frac{c}{3} = \frac{abc}{6}.$$ Hence the second equation $$x^3 + 8y^3 + 27z^3 = 18\,x\,y\,z$$ becomes $$a^3 + b^3 + c^3 = 18\cdot\frac{abc}{6} = 3\,abc.$$
3. Use the identity for three numbers: $$a^3 + b^3 + c^3 - 3abc = \tfrac12(a+b+c)\bigl[(a-b)^2 + (b-c)^2 + (c-a)^2\bigr].$$ For this to be zero with $a+b+c=9>0$, we require $$(a-b)^2 + (b-c)^2 + (c-a)^2 = 0$$ which implies $$a = b = c = \frac{9}{3} = 3.$$
4. Recover $(x,y,z)$: $$x = a = 3,\quad 2y = b = 3\implies y = \tfrac32,\quad 3z = c = 3\implies z = 1.$$

Answer:

$$(x,y,z) = \bigl(3,\tfrac{3}{2},1\bigr).$$