Question

Find DRG and linear expression of

1. $f(x) = sin^{-1}sinx$
2. $f(x)$

Answer 1

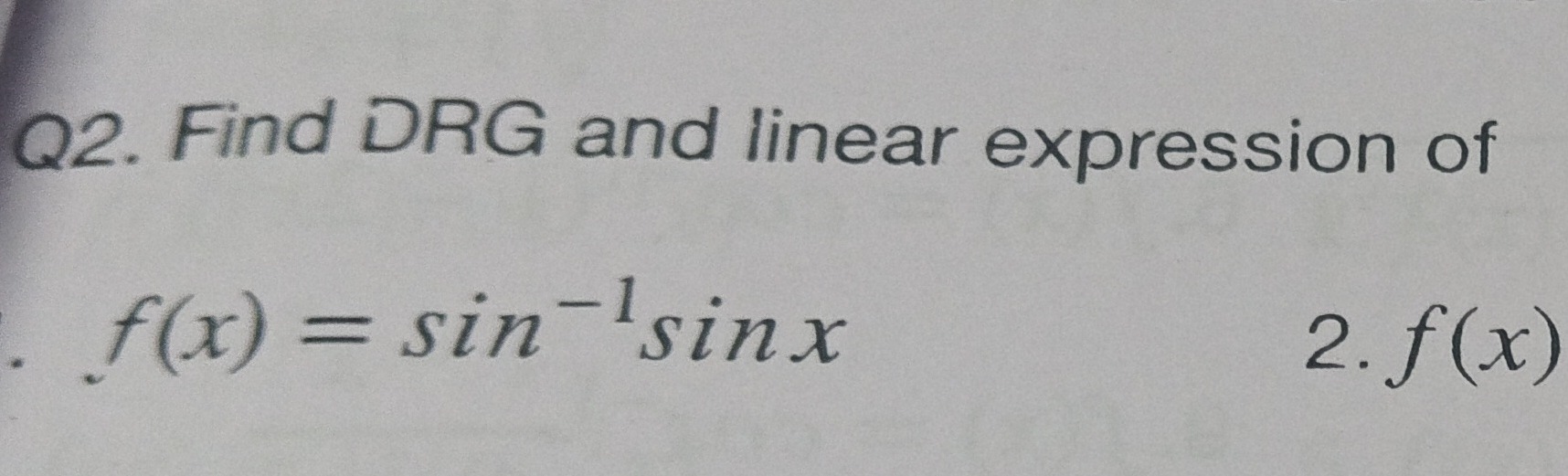
1. DRG of $f(x) = \sin^{-1}(\sin x)$:

   • Domain: $\mathbb{R}$
   • Range: $[-\frac{\pi}{2}, \frac{\pi}{2}]$
   • Graph: Periodic (period $2\pi$), zig-zag wave between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$, with alternating slopes $1$ and $-1$. Passes through $(n\pi, 0)$ for $n \in \mathbb{Z}$.

2. Linear expression of $f(x) = \sin^{-1}(\sin x)$:

   For $x \in [n\pi - \frac{\pi}{2}, n\pi + \frac{\pi}{2}]$, where $n \in \mathbb{Z}$, the linear expression is $f(x) = (-1)^n (x - n\pi)$.

Answer 2

1. Domain: The domain of $\sin x$ is $\mathbb{R}$, and its range is $[-1, 1]$, which is the domain of $\sin^{-1}$. Thus, the domain of $\sin^{-1}(\sin x)$ is $\mathbb{R}$.

2. Range: The range of the principal branch of $\sin^{-1} y$ is $[-\frac{\pi}{2}, \frac{\pi}{2}]$. Thus, the range of $\sin^{-1}(\sin x)$ is $[-\frac{\pi}{2}, \frac{\pi}{2}]$.

3. Graph: The graph of $y = \sin^{-1}(\sin x)$ is a periodic function with period $2\pi$. It consists of line segments with alternating slopes of $1$ and $-1$, forming a zig-zag pattern between $y = -\frac{\pi}{2}$ and $y = \frac{\pi}{2}$. The graph passes through the points $(n\pi, 0)$ for all integers $n$.

4. Linear expression: The linear expression for $\sin^{-1}(\sin x)$ depends on the interval containing $x$. For any integer $n$, if $x$ is in the interval $[n\pi - \frac{\pi}{2}, n\pi + \frac{\pi}{2}]$, the linear expression is given by $\sin^{-1}(\sin x) = (-1)^n (x - n\pi)$.