Question

Dextrorotatory $\alpha$-pinene has a specific rotation $[\alpha]_D^{20} = +51.3^\circ$. A sample of $\alpha$-pinene containing both the enantiomers was found to have a specific rotation value $[\alpha]_D^{20} = +30.8^\circ$. The percentages of the (+) and (-) enantiomers present in the sample are, respectively.

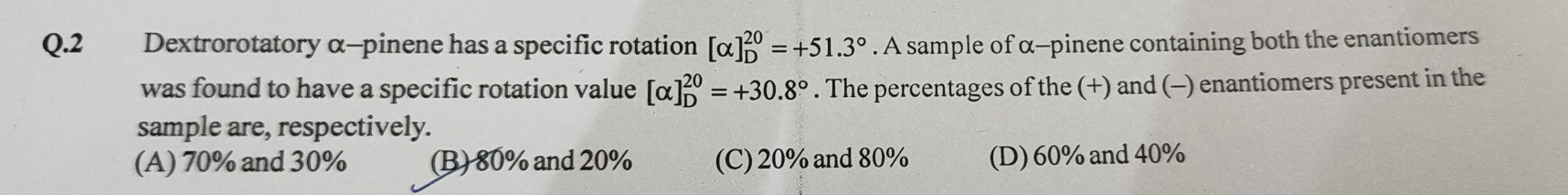
• A. 70% and 30%
• B. 80% and 20%
• C. 20% and 80%
• D. 60% and 40%

Answer 1

Answer: (B)

80% and 20%

Answer 2

Let $[\alpha]_{(+)}$ be the specific rotation of the pure dextrorotatory $\alpha$-pinene, and $[\alpha]_{(-)}$ be the specific rotation of the pure levorotatory $\alpha$-pinene. Given $[\alpha]_{(+)} = +51.3^\circ$. Then $[\alpha]_{(-)} = -51.3^\circ$.

Let the percentage of the (+) enantiomer in the sample be $P_{(+)}$ and the percentage of the (-) enantiomer be $P_{(-)}$. The total percentage is $P_{(+)} + P_{(-)} = 100$.

The observed specific rotation of the mixture, $[\alpha]_{obs}$, is given by the weighted average of the specific rotations of the enantiomers: $[\alpha]_{obs} = \frac{P_{(+)}}{100} [\alpha]_{(+)} + \frac{P_{(-)}}{100} [\alpha]_{(-)}$

Given $[\alpha]_{obs} = +30.8^\circ$. $+30.8 = \frac{P_{(+)}}{100} (+51.3) + \frac{P_{(-)}}{100} (-51.3)$ $+30.8 = \frac{51.3}{100} (P_{(+)} - P_{(-)})$

Rearranging the equation to find the difference in percentages: $P_{(+)} - P_{(-)} = \frac{+30.8 \times 100}{+51.3} = \frac{3080}{51.3}$ $P_{(+)} - P_{(-)} \approx 60.04$

We have a system of two linear equations:

1. $P_{(+)} + P_{(-)} = 100$
2. $P_{(+)} - P_{(-)} \approx 60.04$

Adding equation (1) and equation (2): $(P_{(+)} + P_{(-)}) + (P_{(+)} - P_{(-)}) = 100 + 60.04$ $2 P_{(+)} = 160.04$ $P_{(+)} = \frac{160.04}{2} = 80.02$

Substituting the value of $P_{(+)}$ into equation (1): $80.02 + P_{(-)} = 100$ $P_{(-)} = 100 - 80.02 = 19.98$

The percentages of the (+) and (-) enantiomers are approximately 80.02% and 19.98%, respectively. Rounding to the nearest whole number or matching the options, these values are closest to 80% and 20%.

Alternatively, we can use the concept of enantiomeric excess (ee). The enantiomeric excess is given by the ratio of the observed specific rotation to the specific rotation of the pure enantiomer, multiplied by 100%. $ee = \frac{[\alpha]_{obs}}{[\alpha]_{pure}} \times 100\%$ Since the observed rotation is positive, the (+) enantiomer is in excess, so $[\alpha]_{pure} = [\alpha]_{(+)} = +51.3^\circ$. $ee = \frac{+30.8}{+51.3} \times 100\% \approx 60.04\%$

The enantiomeric excess is also defined as the absolute difference between the mole fractions (or percentages) of the two enantiomers. Since the (+) enantiomer is in excess, $ee = P_{(+)} - P_{(-)}$. $P_{(+)} - P_{(-)} \approx 60.04$

We also know $P_{(+)} + P_{(-)} = 100$. Solving these two equations: $P_{(+)} = \frac{100 + ee}{2} = \frac{100 + 60.04}{2} = \frac{160.04}{2} = 80.02\%$ $P_{(-)} = \frac{100 - ee}{2} = \frac{100 - 60.04}{2} = \frac{39.96}{2} = 19.98\%$

Thus, the percentages of the (+) and (-) enantiomers are approximately 80% and 20%.