Question
Question: If $x^2 + ax + 10 = 0$ and $x^2 + bx - 10 = 0$, have a common root, then $a^2 - b^2$ is equal to...
If x2+ax+10=0 and x2+bx−10=0, have a common root, then a2−b2 is equal to
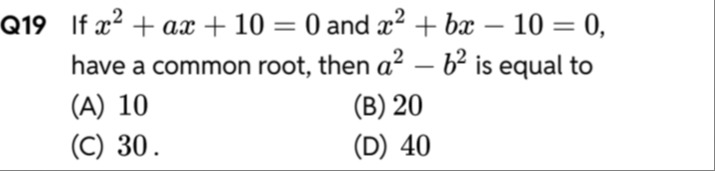
10
20
30
40
40
Solution
Let the common root of the two quadratic equations be α.
Since α is a common root, it must satisfy both equations:
- α2+aα+10=0
- α2+bα−10=0
Subtracting equation (2) from equation (1): (α2+aα+10)−(α2+bα−10)=0
α2+aα+10−α2−bα+10=0
(a−b)α+20=0
(a−b)α=−20…(3)
Adding equation (1) and equation (2): (α2+aα+10)+(α2+bα−10)=0
2α2+aα+bα=0
2α2+(a+b)α=0
α(2α+a+b)=0
This implies two possibilities:
Case 1: α=0
If α=0, substitute it into equation (1):
02+a(0)+10=0
10=0
This is a contradiction, so α cannot be 0.
Case 2: 2α+a+b=0
From this, we get:
a+b=−2α…(4)
We need to find the value of a2−b2. We know that a2−b2=(a−b)(a+b).
From equation (3), since α=0:
a−b=−α20
Substitute the expressions for (a−b) and (a+b) into the identity for a2−b2:
a2−b2=(−α20)(−2α)
a2−b2=α(−20)(−2)α
a2−b2=α40α
a2−b2=40
