Question

If $\log(x-y) - \log 5 - \frac{1}{2}\log x - \frac{1}{2}\log y = 0$ then

$\frac{x}{y} + \frac{y}{x} =$

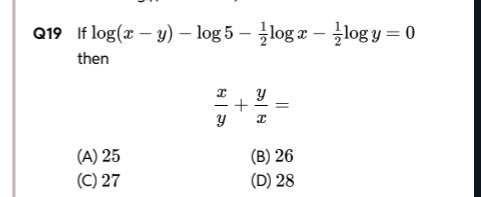
• A. 25
• B. 26
• C. 27
• D. 28

Answer 1

Answer: (C)

27

Answer 2

The given logarithmic equation is $\log(x-y) - \log 5 - \frac{1}{2}\log x - \frac{1}{2}\log y = 0$.

Using logarithm properties $\log A - \log B = \log(A/B)$ and $c \log A = \log(A^c)$, and $\log A + \log B = \log(AB)$:

$\log(x-y) - \log 5 - \frac{1}{2}(\log x + \log y) = 0$

$\log(x-y) - \log 5 - \frac{1}{2}\log(xy) = 0$

$\log(x-y) = \log 5 + \log((xy)^{1/2})$

$\log(x-y) = \log(5\sqrt{xy})$

Equating the arguments:

$x-y = 5\sqrt{xy}$

For the logarithms to be defined, $x>0$, $y>0$, and $x-y>0$, which implies $x>y$.

Divide the equation by $y$ (since $y \neq 0$):

$\frac{x}{y} - 1 = 5\sqrt{\frac{x}{y}}$

Let $t = \sqrt{\frac{x}{y}}$. Since $x>y$, $t>1$. Substituting $t$:

$t^2 - 1 = 5t$

$t^2 - 5t - 1 = 0$

We need to find $\frac{x}{y} + \frac{y}{x}$, which is $t^2 + \frac{1}{t^2}$.

Divide the quadratic equation by $t$ (since $t \neq 0$):

$t - 5 - \frac{1}{t} = 0$

$t - \frac{1}{t} = 5$

Square both sides:

$\left(t - \frac{1}{t}\right)^2 = 5^2$

$t^2 + \frac{1}{t^2} - 2 = 25$

$t^2 + \frac{1}{t^2} = 27$

Thus, $\frac{x}{y} + \frac{y}{x} = 27$.