Question

If $\begin{vmatrix} 1 & a & a \\ b & 1 & b \\ c & c & 1 \end{vmatrix}=0$ where a,b,c are distinct and each $\neq$ 1, then the absolute value of $\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}$ is

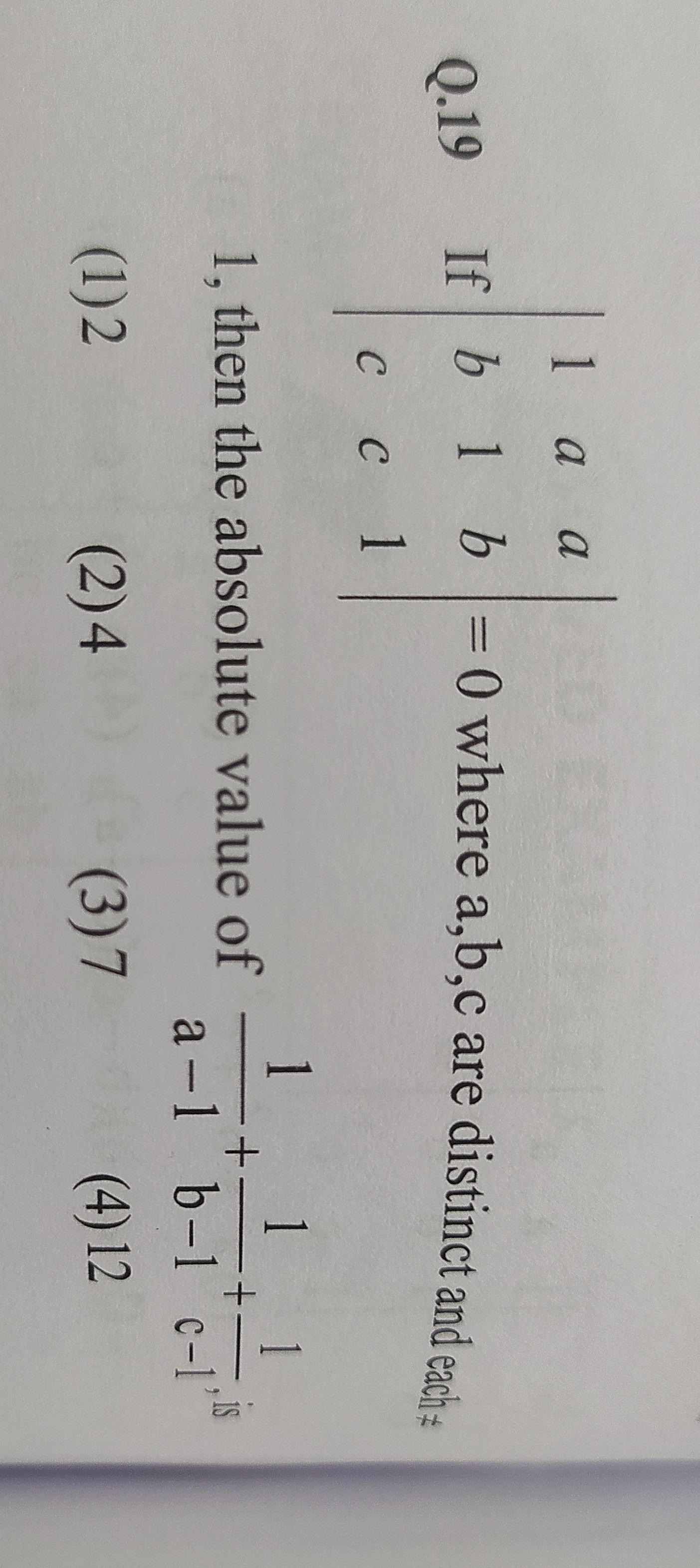
• A. 2
• B. 4
• C. 7
• D. 12

Answer 1

Answer: (A)

2

Answer 2

Given

$$\begin{vmatrix} 1 & a & a\\ b & 1 & b\\ c & c & 1 \end{vmatrix} = 0.$$

Expanding the determinant (by any standard method) we get:

$$1 - ab - ac - bc + 2abc = 0.$$

Let

$$x = a-1,\quad y = b-1,\quad z = c-1.$$

Then, $a=x+1$, $b=y+1$, $c=z+1$. Substitute these into the equation and simplify; after cancellation the equation reduces to:

$$xy + yz + zx + 2xyz = 0.$$

Dividing by $xyz$ (none of $x,y,z$ is zero because $a,b,c\neq1$):

$$\frac{xy+yz+zx}{xyz}+2 = 0 \quad\Rightarrow\quad \frac{1}{x}+\frac{1}{y}+\frac{1}{z} = -2.$$

Thus,

$$\left|\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}\right| = |-2| = 2.$$