Question
Question: Find the value of $\lambda + n$, where $$\lim_{x\to 0} \left( \frac{\cos^2 x - \cos x - e^x \cos x +...
Find the value of λ+n, where limx→0(xncos2x−cosx−excosx+ex−2x3)=λ(∈R−{0});n∈N.
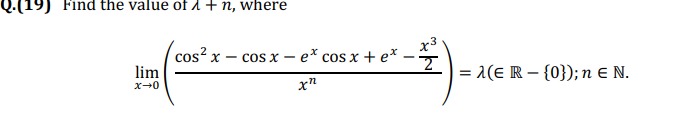
4.5
Solution
The problem asks for the value of λ+n, where n∈N and λ∈R−{0} are defined by the limit: limx→0(xncos2x−cosx−excosx+ex−2x3)=λ
Let the numerator be f(x)=cos2x−cosx−excosx+ex−2x3. As x→0, f(x)→cos20−cos0−e0cos0+e0−203=12−1−1⋅1+1−0=1−1−1+1=0.
Since the limit exists and is a non-zero real number λ, the limit must be of the form 00, and the lowest power of x in the Taylor series expansion of the numerator around x=0 must be xn. The coefficient of xn will be λ.
We use the Taylor series expansions around x=0: cosx=1−2!x2+4!x4−6!x6+8!x8−⋯=1−2x2+24x4−720x6+40320x8−… ex=1+x+2!x2+3!x3+4!x4+5!x5+6!x6+7!x7+8!x8+⋯=1+x+2x2+6x3+24x4+120x5+720x6+5040x7+40320x8+…
Expand each term in the numerator:
-
cos2x=(cosx)2=(1−2x2+24x4−720x6+…)2 =12+(−2x2)2+(24x4)2+2(1)(−2x2)+2(1)(24x4)+2(1)(−720x6)+2(−2x2)(24x4)+2(−2x2)(−720x6)+2(24x4)(−2x2)+… =1−x2+4x4+12x4−360x6−24x6+⋯=1−x2+123+1x4−7202+15x6+⋯=1−x2+31x4−72017x6+…
-
cosx=1−2x2+24x4−720x6+40320x8−…
-
excosx: excosx=1+x−3x3−6x4−30x5+630x7+2520x8+…
-
ex=1+x+2x2+6x3+24x4+120x5+720x6+5040x7+40320x8+…
-
−2x3
Now, assemble f(x)=cos2x−cosx−excosx+ex−2x3: f(x)=(1−x2+31x4−72017x6+4032069x8+…) −(1−2x2+24x4−720x6+40320x8−…) −(1+x−3x3−6x4−30x5+630x7+2520x8+…) +(1+x+2x2+6x3+24x4+120x5+720x6+5040x7+40320x8+…) −2x3
Collect coefficients for each power of x: Constant: 1−1−1+1=0 x1: 0−0−1+1=0 x2: −1−(−21)−0+21=−1+21+21=0 x3: 0−0−(−31)+61−21=31+61−21=62+1−3=0 x4: 31−241−(−61)+241=31−241+61+241=31+61=62+1=63=21 x5: 0−0−(−301)+1201=301+1201=1204+1=1205=241 x6: −72017−(−7201)−0+7201=−72017+7201+7201=720−17+1+1=−72015=−481
So, f(x)=21x4+241x5−481x6−7201x7+4032053x8+…
The lowest power of x with a non-zero coefficient is x4. Thus, n=4. The coefficient of x4 is 21. So, λ=21.
The limit is limx→0xnf(x)=limx→0x421x4+241x5−481x6−…=limx→0(21+241x−481x2−…)=21. So, λ=21 and n=4.
The question asks for the value of λ+n. λ+n=21+4=4.5.
The final answer is 21+4=21+8=29.
