Question
Question: Find the value of $\lambda + n$, where $$\lim_{x\to 0} \left( \frac{\cos^2 x - \cos x - e^x \cos x +...
Find the value of λ+n, where limx→0(xncos2x−cosx−excosx+ex−2x3)=λ(∈R−{0});n∈N.
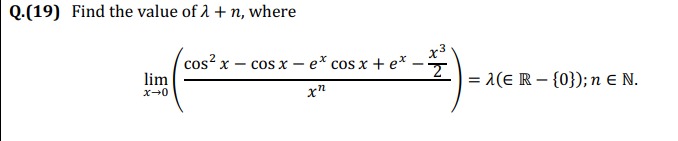
4.5
Solution
Let the given limit be L. L=limx→0(xncos2x−cosx−excosx+ex−2x3) We are given that L=λ, where λ∈R−{0}, and n∈N. For the limit to be a finite non-zero value, the numerator must have a Taylor series expansion around x=0 starting with a term proportional to xn. The terms of order less than n must cancel out.
Let the numerator be N(x)=cos2x−cosx−excosx+ex−2x3. We use the Maclaurin series expansions for the functions involved: cosx=1−2!x2+4!x4−6!x6+O(x8)=1−2x2+24x4−720x6+O(x8) ex=1+x+2!x2+3!x3+4!x4+5!x5+6!x6+O(x7)=1+x+2x2+6x3+24x4+120x5+720x6+O(x7)
Expand each term in the numerator up to a sufficiently high order (let's aim for x6 or x7 since lower order terms are expected to cancel).
cos2x=21+cos(2x)=21+21(1−2!(2x)2+4!(2x)4−6!(2x)6+O(x8)) =21+21(1−2x2+2416x4−72064x6+O(x8)) =21+21−x2+31x4−452x6+O(x8)=1−x2+31x4−452x6+O(x8)
excosx: We can multiply the series expansions: excosx=(1+x+2x2+6x3+24x4+120x5+720x6+O(x7))(1−2x2+24x4−720x6+O(x8)) Collecting terms up to x6: Constant: 1×1=1 x: x×1=x x2: 1×(−2x2)+2x2×1=−2x2+2x2=0 x3: x×(−2x2)+6x3×1=−2x3+6x3=−62x3=−3x3 x4: 1×24x4+2x2×(−2x2)+24x4×1=24x4−4x4+24x4=(241−6+1)x4=−244x4=−6x4 x5: x×24x4+6x3×(−2x2)+120x5×1=24x5−12x5+120x5=(1205−10+1)x5=−1204x5=−30x5 x6: 1×(−720x6)+2x2×24x4+24x4×(−2x2)+720x6×1=−720x6+48x6−48x6+720x6=0 So, excosx=1+x−3x3−6x4−30x5+O(x7)
Now substitute these expansions into N(x): N(x)=(1−x2+31x4−452x6+O(x8)) −(1−2x2+24x4−720x6+O(x8)) −(1+x−3x3−6x4−30x5+O(x7)) +(1+x+2x2+6x3+24x4+120x5+720x6+O(x7)) −2x3
Collect coefficients for each power of x: Constant: 1−1−1+1=0 x: 0−0−1+1=0 x2: −1−(−21)−0+21=−1+21+21=0 x3: 0−0−(−31)+61−21=31+61−21=62+1−3=0 x4: 31−241−(−61)+241=31−241+61+241=31+61=62+1=63=21 x5: 0−0−(−301)+1201=301+1201=1204+1=1205=241 x6: −452−(−7201)−0+7201=−452+7201+7201=−72032+7201+7201=720−32+2=−72030=−241
So, N(x)=21x4+241x5−241x6+O(x7).
The limit is L=limx→0xnN(x)=limx→0xn21x4+241x5−241x6+O(x7). For the limit to be a finite non-zero value λ, the lowest power of x in the numerator must match the power of x in the denominator. The lowest power of x in N(x) is x4. Thus, n must be 4.
Substituting n=4: L=limx→0x421x4+241x5−241x6+O(x7)=limx→0(21+241x−241x2+O(x3)) As x→0, the limit is 21. So, λ=21.
We are asked to find the value of λ+n. λ+n=21+4=4.5.
Alternatively, we could use L'Hopital's rule, but the derivatives become increasingly complex. Let N(x)=cos2x−cosx−excosx+ex−2x3. N(0)=cos20−cos0−e0cos0+e0−203=12−1−1×1+1−0=1−1−1+1=0. N′(x)=2cosx(−sinx)−(−sinx)−(excosx+ex(−sinx))+ex−23x2 N′(x)=−2sinxcosx+sinx−excosx+exsinx+ex−23x2 N′(0)=−2(0)(1)+0−1(1)+1(0)+1−0=−1+1=0. N′′(x)=−2(cos2x−sin2x)+cosx−(excosx−exsinx+exsinx+excosx)+ex−3x N′′(x)=−2cos(2x)+cosx−(2excosx)+ex−3x N′′(0)=−2cos(0)+cos(0)−2e0cos(0)+e0−0=−2(1)+1−2(1)(1)+1=−2+1−2+1=−2. Since N′′(0)=0, the lowest power of x in the numerator expansion should be x2. However, our Taylor series expansion showed the lowest power is x4. Let's recheck the derivatives.
N(x)=cos2x−cosx−excosx+ex−2x3 N′(x)=2cosx(−sinx)−(−sinx)−(excosx−exsinx)+ex−23x2 N′(x)=−sin(2x)+sinx−excosx+exsinx+ex−23x2 N′(0)=0+0−1(1)+1(0)+1−0=−1+1=0. Correct.
N′′(x)=−2cos(2x)+cosx−(excosx−exsinx)+(exsinx+excosx)+ex−3x N′′(x)=−2cos(2x)+cosx−excosx+exsinx+exsinx+excosx+ex−3x N′′(x)=−2cos(2x)+cosx+2exsinx+ex−3x N′′(0)=−2cos(0)+cos(0)+2e0sin(0)+e0−0=−2(1)+1+2(1)(0)+1=−2+1+0+1=0. Correct.
N′′′(x)=−2(−sin(2x)⋅2)−sinx+(2exsinx+2excosx)+ex−3 N′′′(x)=4sin(2x)−sinx+2exsinx+2excosx+ex−3 N′′′(0)=4sin(0)−sin(0)+2e0sin(0)+2e0cos(0)+e0−3=0−0+0+2(1)(1)+1−3=2+1−3=0. Correct.
N(4)(x)=4(cos(2x)⋅2)−cosx+(2exsinx+2excosx)+(2excosx−2exsinx)+ex N(4)(x)=8cos(2x)−cosx+4excosx+ex N(4)(0)=8cos(0)−cos(0)+4e0cos(0)+e0=8(1)−1+4(1)(1)+1=8−1+4+1=12.
Wait, according to the Taylor series N(x)=4!N(4)(0)x4+O(x5). The coefficient of x4 is 4!12=2412=21. This matches the Taylor series expansion result.
The limit is L=limx→0xnN(x). Since N(x)=21x4+O(x5), for the limit to be a non-zero finite value, we must have n=4. L=limx→0x421x4+O(x5)=limx→0(21+O(x))=21. So, n=4 and λ=21.
The value of λ+n=21+4=4.5.
The final answer is λ+n=4.5.
The final answer is 4.5.
