Question
Question: If the equation $x^2 - (p+q)x + 4 = 0; x^2 - 2qx + 8 = 0$ and $x^2 - (2p+q)x + 12 = 0$ have exactly...
If the equation x2−(p+q)x+4=0;x2−2qx+8=0 and x2−(2p+q)x+12=0 have exactly
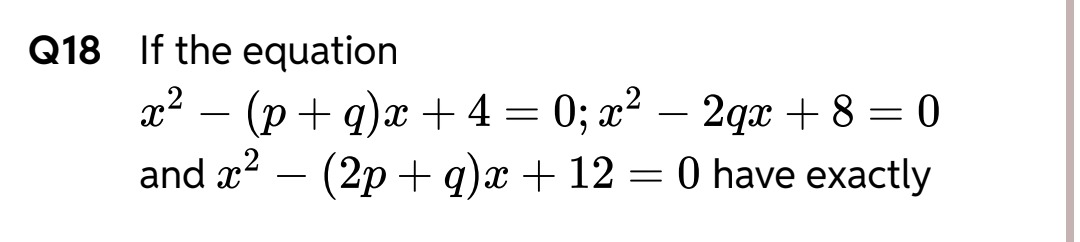
6
Solution
The problem statement is incomplete, ending with "have exactly". Based on the typical structure of such problems in competitive exams like JEE/NEET, it is highly probable that the question implies "have exactly one common root" and asks for a specific value related to the parameters p and q, or the common root itself. We will proceed by finding the conditions for these three quadratic equations to have a common root.
Let the common root be α. Substituting α into each equation, we get:
- α2−(p+q)α+4=0(I)
- α2−2qα+8=0(II)
- α2−(2p+q)α+12=0(III)
Subtract equation (I) from equation (II): (α2−2qα+8)−(α2−(p+q)α+4)=0 α2−2qα+8−α2+pα+qα−4=0 pα−qα+4=0 (p−q)α=−4(IV)
Subtract equation (II) from equation (III): (α2−(2p+q)α+12)−(α2−2qα+8)=0 α2−2pα−qα+12−α2+2qα−8=0 −2pα+qα+4=0 (−2p+q)α=−4(V)
From equations (IV) and (V), we have: (p−q)α=−4 (−2p+q)α=−4
Since the right-hand sides are equal, the left-hand sides must be equal: (p−q)α=(−2p+q)α
If α=0, then from (IV) we get 0=−4, which is a contradiction. Therefore, α=0. Since α=0, we can divide both sides by α: p−q=−2p+q 3p=2q q=23p
Now substitute q=23p into equation (IV): (p−23p)α=−4 (−21p)α=−4 pα=8
From pα=8, we can express p as p=α8. Then, q=23p=23(α8)=α12.
Substitute these expressions for p and q in terms of α into any of the original equations. Let's use equation (I): α2−(p+q)α+4=0 α2−(α8+α12)α+4=0 α2−(α20)α+4=0 α2−20+4=0 α2−16=0 α2=16 α=±4
Now we have two possible values for the common root α:
Case 1: α=4 Using p=α8 and q=α12: p=48=2 q=412=3 In this case, the product pq=2×3=6.
The equations become:
- x2−(2+3)x+4=0⟹x2−5x+4=0⟹(x−1)(x−4)=0. Roots are 1,4.
- x2−2(3)x+8=0⟹x2−6x+8=0⟹(x−2)(x−4)=0. Roots are 2,4.
- x2−(2(2)+3)x+12=0⟹x2−7x+12=0⟹(x−3)(x−4)=0. Roots are 3,4. All three equations have exactly one common root, which is 4.
Case 2: α=−4 Using p=α8 and q=α12: p=−48=−2 q=−412=−3 In this case, the product pq=(−2)×(−3)=6.
The equations become:
- x2−(−2−3)x+4=0⟹x2+5x+4=0⟹(x+1)(x+4)=0. Roots are −1,−4.
- x2−2(−3)x+8=0⟹x2+6x+8=0⟹(x+2)(x+4)=0. Roots are −2,−4.
- x2−(2(−2)+(−3))x+12=0⟹x2+7x+12=0⟹(x+3)(x+4)=0. Roots are −3,−4. All three equations have exactly one common root, which is −4.
In both valid scenarios, the product pq is 6. This makes pq=6 a unique value, which is often the expected answer for such problems when the common root itself is not unique.
