Question

If the equation $ax^2 + bx + c = 0$ has the same roots as $px^2 + qx + r = 0 (a,b,c,p,q,r \in R \text{ and all non zero})$, sho

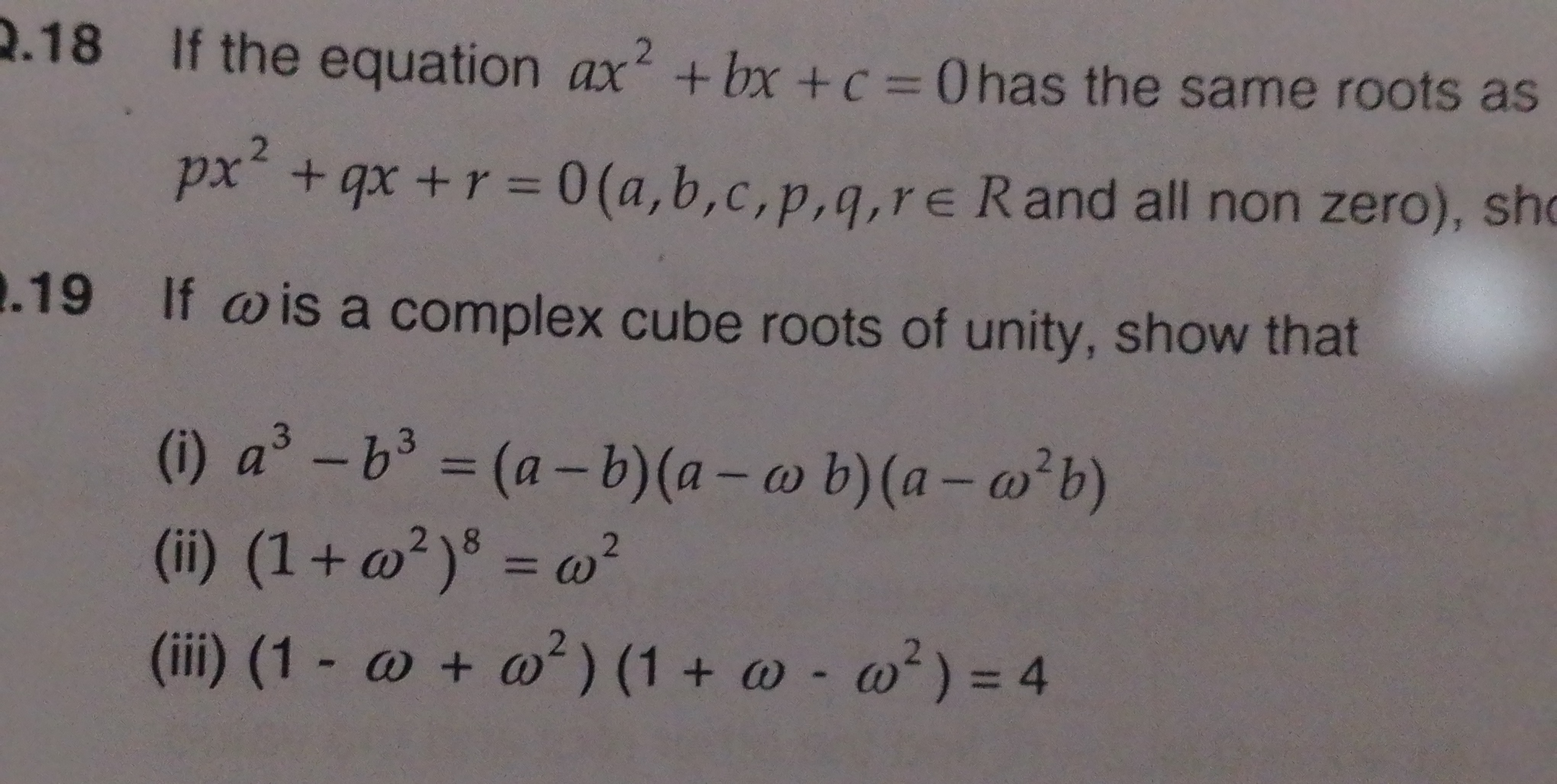
Answer 1

If $ax^2 + bx + c = 0$ and $px^2 + qx + r = 0$ have the same roots, then $\frac{a}{p} = \frac{b}{q} = \frac{c}{r}$.

Answer 2

If two quadratic equations $ax^2 + bx + c = 0$ and $px^2 + qx + r = 0$ have the same roots, then their coefficients are proportional. This is shown by equating the sum and product of roots from Vieta's formulas for both equations, leading to the relation $\frac{a}{p} = \frac{b}{q} = \frac{c}{r}$.