Question

Q.18 If $C = \sum_{k=1}^{35} \cos{(5k)^\circ}$ and $S = \sum_{k=1}^{36} \sin{(10k)^\circ}$ then find $(C^2 + S^2)$.

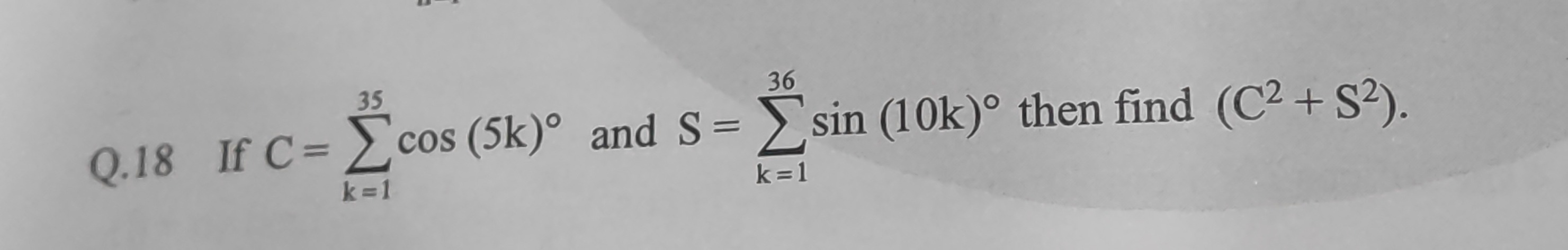
Answer 1

0

Answer 2

Explanation (Minimal):
For $C = \sum_{k=1}^{35} \cos(5k^\circ)$, using the formula

$$\sum_{k=1}^{n} \cos k\theta = \frac{\sin\left(\frac{n\theta}{2}\right)\cos\left(\frac{(n+1)\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)},$$

with $n=35$ and $\theta = 5^\circ$ gives

$$C = \frac{\sin(87.5^\circ)\cos(90^\circ)}{\sin(2.5^\circ)} = 0 \quad (\text{since } \cos(90^\circ)=0).$$

Similarly, for

$$S = \sum_{k=1}^{36} \sin(10k^\circ),$$

using the sum formula

$$\sum_{k=1}^{n} \sin k\theta = \frac{\sin\left(\frac{n\theta}{2}\right)\sin\left(\frac{(n+1)\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)},$$

with $n=36$ and $\theta = 10^\circ$ gives

$$S = \frac{\sin(180^\circ)\sin(185^\circ)}{\sin(5^\circ)} = 0 \quad (\text{since } \sin(180^\circ)=0).$$

Thus,

$$C^2 + S^2 = 0^2 + 0^2 = 0.$$