Question

Two equal sides of an isosceles triangle are given by the equations $7x-y+3=0$ and $x+y-3=0$ & its third side passes through the point $(1, -10)$. Determine the equation of the third side.

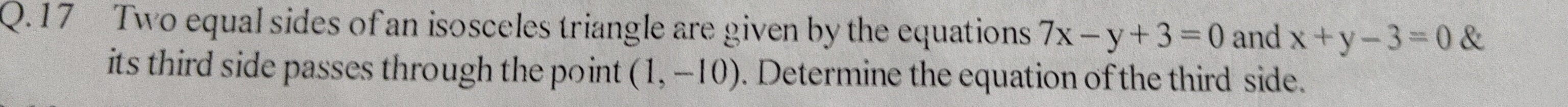
• A. x - 3y - 31 = 0
• B. 3x + y + 7 = 0

Answer 1

Answer: (B)

3x+y+7=0

Answer 2

Let the equations of the two equal sides be $L_1: 7x - y + 3 = 0$ and $L_2: x + y - 3 = 0$. Let the equation of the third side (the base) be $L_3$. The third side passes through the point $P(1, -10)$.

1. Find the slopes of the given sides:

The slope of $L_1$ is $m_1 = 7$. The slope of $L_2$ is $m_2 = -1$.

2. Use the property of isosceles triangles:

In an isosceles triangle, the angles made by the equal sides with the base are equal. Let the slope of the third side be $m_3$. The angle between $L_1$ and $L_3$ is equal to the angle between $L_2$ and $L_3$. Using the formula for the angle between two lines, $\tan \theta = \left| \frac{m_a - m_b}{1 + m_a m_b} \right|$:

$$\left| \frac{m_1 - m_3}{1 + m_1 m_3} \right| = \left| \frac{m_2 - m_3}{1 + m_2 m_3} \right|$$

Substitute $m_1 = 7$ and $m_2 = -1$:

$$\left| \frac{7 - m_3}{1 + 7m_3} \right| = \left| \frac{-1 - m_3}{1 - m_3} \right|$$

This leads to two cases:

Case 1: $\frac{7 - m_3}{1 + 7m_3} = \frac{-1 - m_3}{1 - m_3}$

$(7 - m_3)(1 - m_3) = (-1 - m_3)(1 + 7m_3)$

$7 - 8m_3 + m_3^2 = -1 - 8m_3 - 7m_3^2$

$8m_3^2 + 8 = 0 \implies m_3^2 = -1$

This equation has no real solution for $m_3$. This case corresponds to the angle bisector being perpendicular to one of the lines, which is not possible for the base of an isosceles triangle.

Case 2: $\frac{7 - m_3}{1 + 7m_3} = - \left( \frac{-1 - m_3}{1 - m_3} \right) = \frac{1 + m_3}{1 - m_3}$

$(7 - m_3)(1 - m_3) = (1 + m_3)(1 + 7m_3)$

$7 - 8m_3 + m_3^2 = 1 + 8m_3 + 7m_3^2$

$6m_3^2 + 16m_3 - 6 = 0$

$3m_3^2 + 8m_3 - 3 = 0$

Solve the quadratic equation for $m_3$:

$m_3 = \frac{-8 \pm \sqrt{8^2 - 4(3)(-3)}}{2(3)}$

$m_3 = \frac{-8 \pm \sqrt{64 + 36}}{6}$

$m_3 = \frac{-8 \pm \sqrt{100}}{6}$

$m_3 = \frac{-8 \pm 10}{6}$

This gives two possible values for $m_3$:

$m_3 = \frac{-8 + 10}{6} = \frac{2}{6} = \frac{1}{3}$

$m_3 = \frac{-8 - 10}{6} = \frac{-18}{6} = -3$

3. Find the equation of the third side using the point-slope form:

The third side passes through $P(1, -10)$. Using $y - y_1 = m(x - x_1)$:

Possibility A: $m_3 = \frac{1}{3}$

$y - (-10) = \frac{1}{3}(x - 1)$

$y + 10 = \frac{1}{3}(x - 1)$

$3(y + 10) = x - 1$

$3y + 30 = x - 1$

$x - 3y - 31 = 0$

Possibility B: $m_3 = -3$

$y - (-10) = -3(x - 1)$

$y + 10 = -3x + 3$

$3x + y + 7 = 0$

4. Check for validity (optional but good practice):

The vertex formed by $L_1$ and $L_2$ is found by solving their equations:

$7x - y + 3 = 0$

$x + y - 3 = 0$

Adding the two equations: $8x = 0 \implies x = 0$. Substituting $x=0$ into the second equation: $0 + y - 3 = 0 \implies y = 3$. So, the vertex is $V(0, 3)$.

The third side (base) should not pass through the vertex $V(0,3)$.

For $x - 3y - 31 = 0$: $0 - 3(3) - 31 = -9 - 31 = -40 \neq 0$.

For $3x + y + 7 = 0$: $3(0) + 3 + 7 = 10 \neq 0$.

Both possibilities are valid in this regard.

Also, the third side should not be parallel to either of the equal sides. $m_1 = 7$, $m_2 = -1$. Neither $1/3$ nor $-3$ is equal to $7$ or $-1$. Both possibilities are valid.

The problem typically implies a unique solution in such contexts. In geometry, the "third side" of an isosceles triangle refers to the base. The base is perpendicular to the internal angle bisector of the vertex angle. The slopes $1/3$ and $-3$ are negative reciprocals of each other, meaning the two possible lines for $L_3$ are perpendicular. This corresponds to the two angle bisectors of $L_1$ and $L_2$ also being perpendicular. One of these angle bisectors is the internal one, and the other is the external one. The base must be perpendicular to the internal angle bisector.

The equations of the angle bisectors of $L_1$ and $L_2$ are:

$\frac{7x - y + 3}{\sqrt{7^2 + (-1)^2}} = \pm \frac{x + y - 3}{\sqrt{1^2 + 1^2}}$

$\frac{7x - y + 3}{5\sqrt{2}} = \pm \frac{x + y - 3}{\sqrt{2}}$

$\frac{7x - y + 3}{5} = \pm (x + y - 3)$

Bisector 1 (internal): $7x - y + 3 = 5(x + y - 3) \implies 2x - 6y + 18 = 0 \implies x - 3y + 9 = 0$. Slope $m_{B_1} = 1/3$.

Bisector 2 (external): $7x - y + 3 = -5(x + y - 3) \implies 12x + 4y - 12 = 0 \implies 3x + y - 3 = 0$. Slope $m_{B_2} = -3$.

The base of the isosceles triangle is perpendicular to the internal angle bisector of the vertex angle.

To determine the internal bisector, we can check a point. Let's take the origin $(0,0)$.

For $L_1: 7(0) - 0 + 3 = 3$

For $L_2: 0 + 0 - 3 = -3$

Since the signs are opposite, the origin $(0,0)$ lies in the angle containing the origin.

For $B_1: 0 - 3(0) + 9 = 9$.

For $B_2: 3(0) + 0 - 3 = -3$.

The internal bisector is the one for which the signs for $L_1$ and $L_2$ are opposite, and its value for the point $(0,0)$ has a sign that places it in the correct region.

A simpler way to identify the internal bisector is to choose the one whose slope is between $m_1$ and $m_2$. $m_1=7$, $m_2=-1$. $m_{B_1}=1/3$ is between $-1$ and $7$. $m_{B_2}=-3$ is not. So $B_1: x - 3y + 9 = 0$ is the internal angle bisector.

The slope of the base ($L_3$) must be perpendicular to the slope of the internal angle bisector $B_1$. Slope of $B_1$ is $1/3$. Therefore, the slope of $L_3$ must be $m_3 = -1/(1/3) = -3$. This corresponds to Possibility B.

The equation of the third side is $3x + y + 7 = 0$.