Question

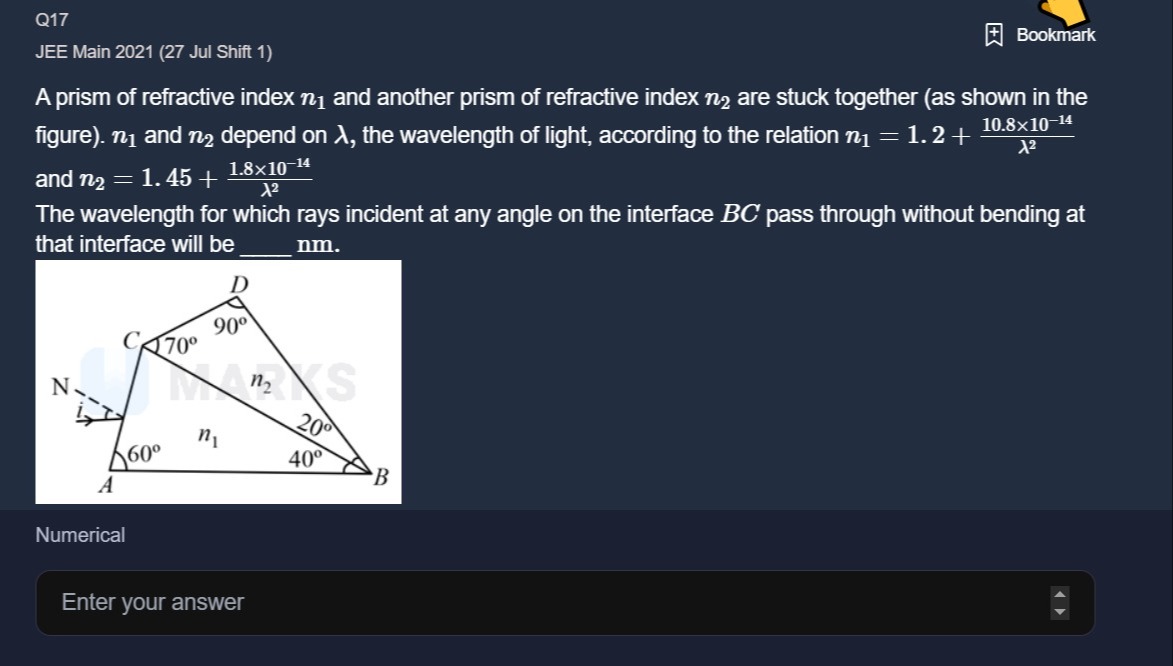
A prism of refractive index $n_1$ and another prism of refractive index $n_2$ are stuck together (as shown in the figure). $n_1$ and $n_2$ depend on $\lambda$, the wavelength of light, according to the relation $n_1 = 1.2 + \frac{10.8 \times 10^{-14}}{\lambda^2}$ and $n_2 = 1.45 + \frac{1.8 \times 10^{-14}}{\lambda^2}$

The wavelength for which rays incident at any angle on the interface $BC$ pass through without bending at that interface will be ______ nm.

Answer 1

600 nm

Answer 2

We require that light passes from one prism to the other without bending at the interface. This implies that the light sees no change in refractive index, i.e., $n_1 = n_2$.

Given:

$$n_1 = 1.2 + \frac{10.8\times10^{-14}}{\lambda^2}, \quad n_2 = 1.45 + \frac{1.8\times10^{-14}}{\lambda^2}.$$

Setting $n_1 = n_2$:

$$1.2 + \frac{10.8\times10^{-14}}{\lambda^2} = 1.45 + \frac{1.8\times10^{-14}}{\lambda^2}.$$

Rearrange:

$$\frac{10.8\times10^{-14} - 1.8\times10^{-14}}{\lambda^2} = 1.45 - 1.2.$$

Simplify:

$$\frac{9.0\times10^{-14}}{\lambda^2} = 0.25.$$

Solve for $\lambda^2$:

$$\lambda^2 = \frac{9.0\times10^{-14}}{0.25} = 36\times10^{-14} = 3.6\times10^{-13}.$$

Taking the square root:

$$\lambda = \sqrt{3.6\times10^{-13}} = 6.0\times10^{-7}\, \text{m} = 600\, \text{nm}.$$