Question
Question: Charge $q_1$ = + 6.0 nC is on Y- axis at y=+3 cm and charge $q_2$=-6.0 nC is on Y- axis at y=-3 cm c...
Charge q1 = + 6.0 nC is on Y- axis at y=+3 cm and charge q2=-6.0 nC is on Y- axis at y=-3 cm calculate force on a test charge q0 = 2nC placed on X-axis at x=4 cm.
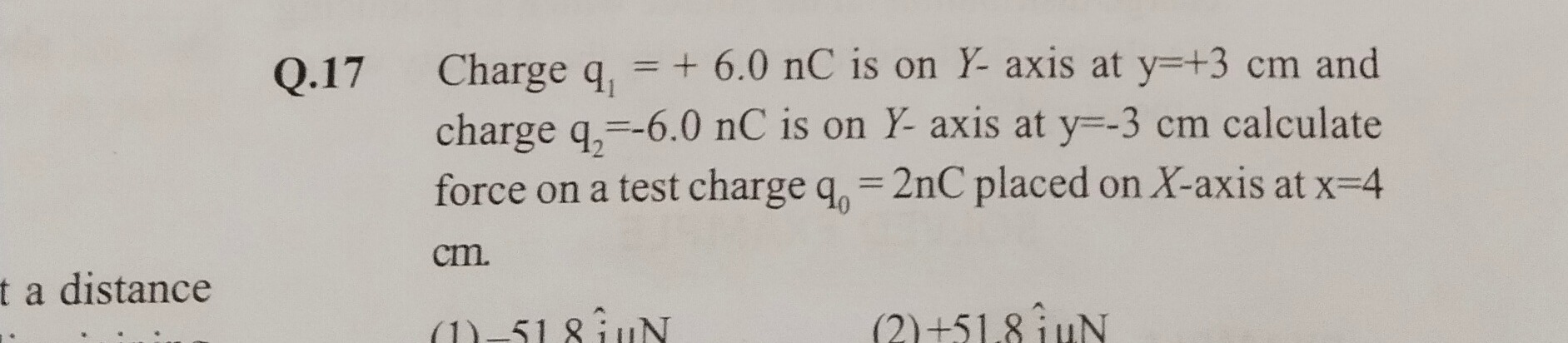
-51.8 i^ μN
+51.8 i^ μN
The net force on q0 is approximately 51.8μN downward (i.e. along −j^); none of the given options are correct.
Solution
Solution
We are given
q1=+6.0nCat(0,+0.03m),q2=−6.0nCat(0,−0.03m),q0=+2.0nCat(0.04m,0).For any two charges the Coulomb force is
F=kr2∣qaqb∣with k=9×109N m2/C2.Step 1. Compute distance:
Distance from either q1 or q2 to q0
Step 2. Magnitude of force from each charge:
F=(0.05)29×109×(2×10−9)(6×10−9)=0.00259×109×12×10−18=43.2μN.Step 3. Directions
For q1 (positive):
Since like charges repel, the force on q0 is along
Its unit vector is
(0.050.04,0.05−0.03)=(0.8,−0.6).Thus,
F1=43.2(0.8i^−0.6j^)=(34.56i^−25.92j^)μN.For q2 (negative):
Since opposite charges attract, the force on q0 is directed toward q2. That is,
with unit vector
(−0.8,−0.6).Thus,
F2=43.2(−0.8i^−0.6j^)=(−34.56i^−25.92j^)μN.Step 4. Net force
F=F1+F2=(34.56−34.56)i^+(−25.92−25.92)j^=(0i^,−51.84j^)μN.Thus, the net force is about 51.8μN downward along the negative y–axis.
Note on the Given Options
The options provided are
- −51.8i^μN
- +51.8i^μN
Both options suggest a force in the x–direction. However, our result shows the force is purely vertical (along −j^). Hence, neither option is correct.
Final Answer:
The net force on q0 is approximately 51.8μN downward (i.e. along −j^); none of the given options are correct.
Summary of Details:
-
Explanation (Minimal):
- Calculate the distance r=0.05m from each charge to the test charge.
- Find force magnitude: F=43.2μN from each charge using Coulomb’s law.
- For q1 the force is repulsive (directed along (0.04,−0.03) → unit vector (0.8,−0.6)); for q2 the force is attractive (directed along (−0.04,−0.03) → unit vector (−0.8,−0.6)).
- Adding forces gives: F=(34.56−34.56)i^+(−25.92−25.92)j^=(0,−51.84)μN.
-
Answer: The net force is 51.8μN downward (along −j^); hence, none of the provided options [(1) and (2)] are correct.
