Question
Question: Let $M = \begin{bmatrix} x & 2x & 3x \\ f(x) & g(x) & h(x) \\ 0 & 1 & 1 \end{bmatrix}$ be a singular...
Let M=xf(x)02xg(x)13xh(x)1 be a singular matrix. If f(x)=ln(ex+1) and g(x)=ln(ex−1), then the value of h'(ln 3) is
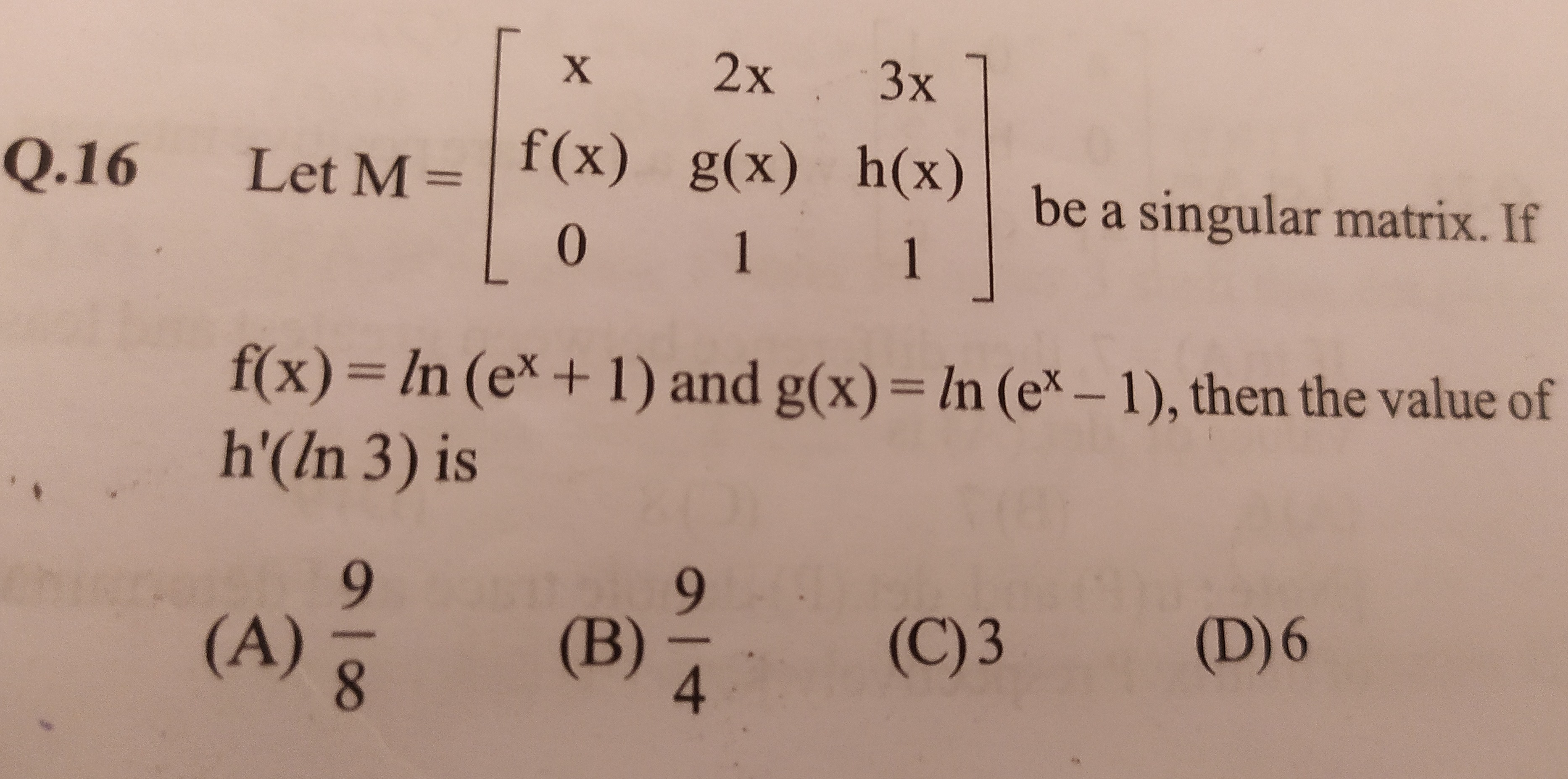
89
49
3
6
49
Solution
The given matrix is M=xf(x)02xg(x)13xh(x)1. The matrix M is singular, which means its determinant is zero, i.e., det(M)=0. The determinant of M is calculated as:
det(M)=xg(x)1h(x)1−2xf(x)0h(x)1+3xf(x)0g(x)1
det(M)=x(g(x)⋅1−h(x)⋅1)−2x(f(x)⋅1−h(x)⋅0)+3x(f(x)⋅1−g(x)⋅0)
det(M)=x(g(x)−h(x))−2xf(x)+3xf(x)
det(M)=x(g(x)−h(x)+f(x))
Since det(M)=0, we have x(g(x)−h(x)+f(x))=0.
The functions are f(x)=ln(ex+1) and g(x)=ln(ex−1). The function g(x) is defined for ex−1>0, which means ex>1, or x>0. The relation holds for x>0.
For x>0, we can divide by x:
g(x)−h(x)+f(x)=0
h(x)=f(x)+g(x)
Substitute the expressions for f(x) and g(x):
h(x)=ln(ex+1)+ln(ex−1)
Using the logarithm property lnA+lnB=ln(AB):
h(x)=ln((ex+1)(ex−1))
Using the difference of squares formula (a+b)(a−b)=a2−b2:
h(x)=ln((ex)2−12)=ln(e2x−1)
This expression for h(x) is valid for x>0.
Next, we need to find the derivative of h(x), denoted by h′(x).
h(x)=ln(e2x−1)
Using the chain rule, dxdln(u)=u1dxdu. Let u=e2x−1.
dxdu=dxd(e2x−1)=e2x⋅dxd(2x)−0=e2x⋅2=2e2x.
So, h′(x)=e2x−11⋅2e2x=e2x−12e2x.
Finally, we need to evaluate h′(ln3). Substitute x=ln3 into the expression for h′(x). Note that ln3>0, so it is in the domain of h′(x).
h′(ln3)=e2(ln3)−12e2(ln3)
Using the logarithm and exponent properties alnb=lnba and elnc=c:
2ln3=ln32=ln9.
So, e2(ln3)=eln9=9.
Substitute this value into the expression for h′(ln3):
h′(ln3)=9−12⋅9=818=49.
The value of h′(ln3) is 49.
