Question
Question: Given two series S₁ = 1 - $\frac{1}{2}$ + $\frac{1}{3}$ - $\frac{1}{4}$ +.....+ $\frac{1}{2019}$ and...
Given two series S₁ = 1 - 21 + 31 - 41 +.....+ 20191 and S₂ = 10101 + 10111 + 10121 +.....+ 20191, then
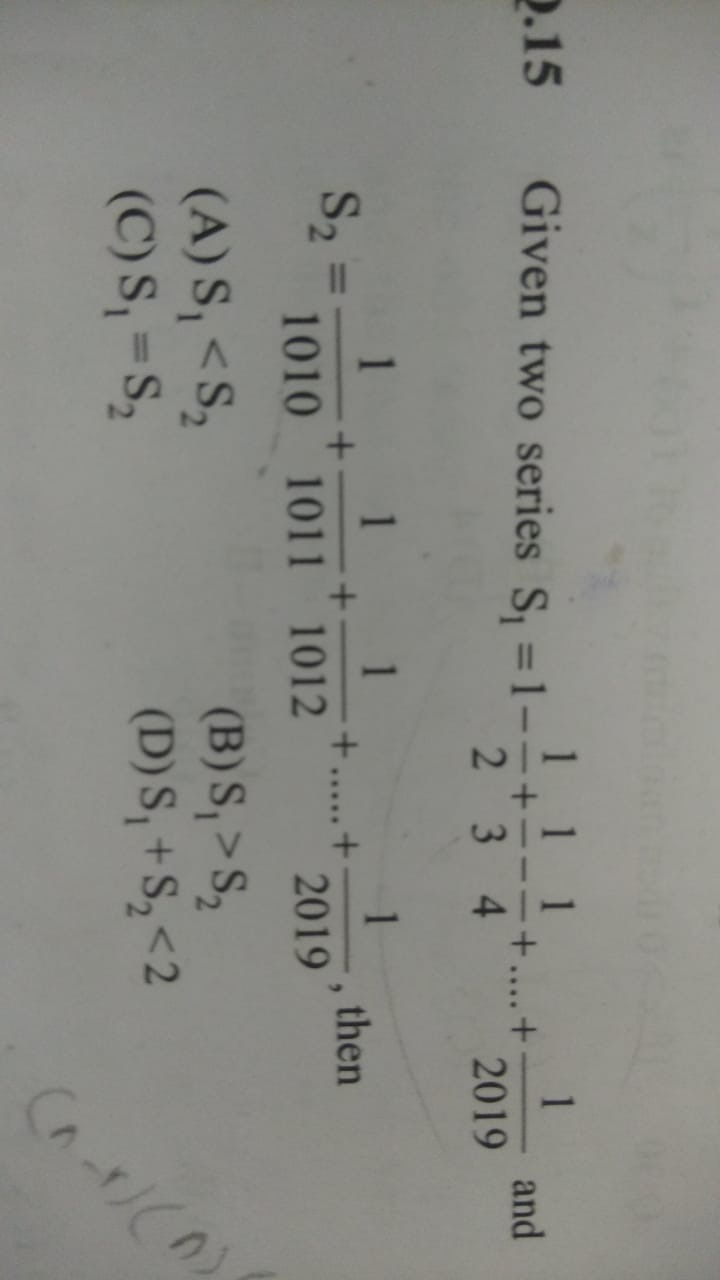
S₁ < S₂
S₁ > S₂
S₁ = S₂
S₁+S₂ < 2
C
Solution
The series S₁ can be written as: S1=1−21+31−41+⋯+20191
We can rewrite S₁ by grouping terms: S1=(1+31+51+⋯+20191)−(21+41+61+⋯+20181)
To relate this to the harmonic series (Hn=1+21+31+⋯+n1), we can add and subtract the even terms: S1=(1+21+31+41+⋯+20191)−2(21+41+⋯+20181) S1=H2019−2⋅21(1+21+⋯+10091) S1=H2019−H1009
Now, expanding H2019−H1009: H2019=(1+21+⋯+10091)+(10101+10111+⋯+20191) H1009=1+21+⋯+10091 So, H2019−H1009=(10101+10111+⋯+20191).
This is precisely the series S₂. Thus, S1=S2.
Now consider S1+S2<2. Since S1=S2, this inequality becomes 2S1<2, or S1<1. Let's check if S1<1: S1=1−(21−31)−(41−51)−⋯−(20181−20191) Each term in parentheses is positive, e.g., (21−31)=61. Therefore, S1=1−(a sum of positive terms), which implies S1<1. Consequently, S1+S2<2 is also true.
Both options (C) and (D) are correct. However, option (C) establishes the direct equality between the two series, which is the primary relationship derived.
