Question
Question: A current is flowing in a regular hexagon wire of side a. The magnetic field at the centre O is ...
A current is flowing in a regular hexagon wire of side a. The magnetic field at the centre O is
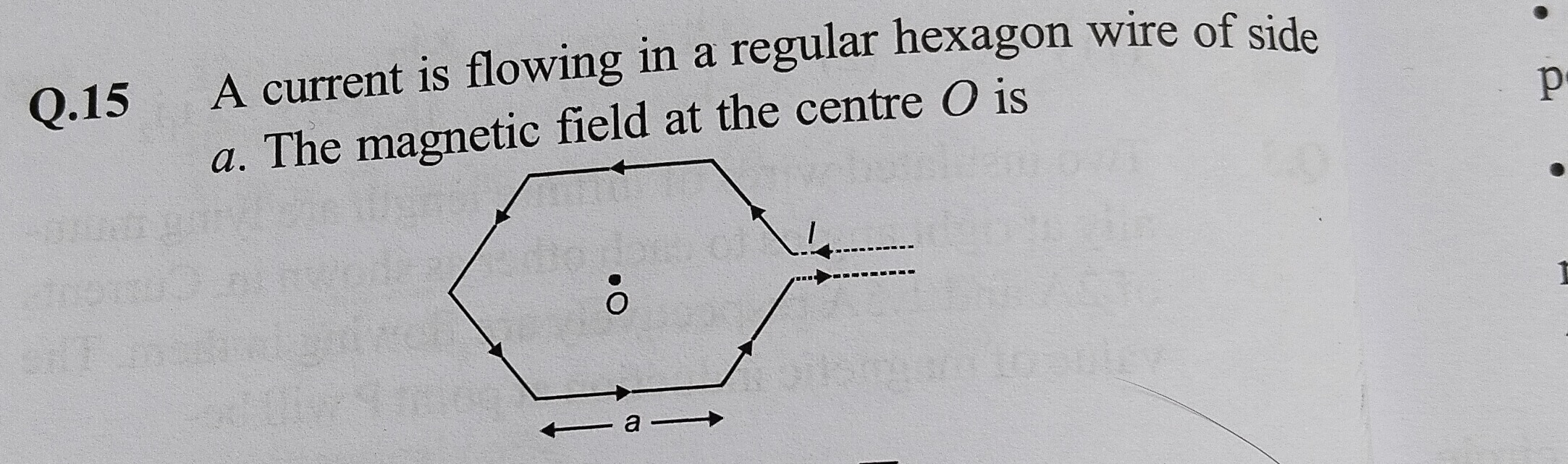
πa3μ0I
Solution
To find the magnetic field at the center O of a regular hexagonal wire of side 'a' carrying current 'I', we can sum the magnetic fields produced by each of the six straight wire segments.
-
Magnetic field due to a single straight wire segment: The magnetic field (B) due to a finite straight current-carrying wire at a point P is given by: B=4πrμ0I(sinϕ1+sinϕ2) where:
- μ0 is the permeability of free space.
- I is the current flowing in the wire.
- r is the perpendicular distance from the point P to the wire.
- ϕ1 and ϕ2 are the angles made by the lines connecting the point P to the ends of the wire segment, with the perpendicular line from P to the wire.
-
Geometry of a regular hexagon:
- A regular hexagon has 6 equal sides.
- The center O of a regular hexagon is equidistant from all its vertices and all its sides.
- A regular hexagon can be divided into 6 equilateral triangles by drawing lines from the center to each vertex. The side length of these equilateral triangles is equal to the side length of the hexagon, 'a'.
- Consider one side of the hexagon. Let its length be 'a'. The lines from the center O to the two ends of this side form an equilateral triangle with the side.
- Therefore, the angle subtended by each side at the center O is 60∘.
-
Determine r, ϕ1, and ϕ2 for one side:
- The perpendicular distance 'r' from the center O to the midpoint of any side is the altitude of one of the equilateral triangles.
- In an equilateral triangle of side 'a', the altitude (r) is given by: r=asin(60∘)=a23
- Now, consider the angles ϕ1 and ϕ2. These are the angles made by the lines connecting the center O to the ends of the wire segment, with the perpendicular line from O to the wire. Since the triangle formed by the center O and the two ends of the side is equilateral, the angles at the base (at the ends of the side) are 60∘. The line from O to the midpoint of the side is perpendicular to the side and bisects the angle at O. Thus, ϕ1=ϕ2=60∘/2=30∘.
-
Calculate magnetic field due to one side: Substitute the values of r, ϕ1, and ϕ2 into the formula for Bside: Bside=4πrμ0I(sin(30∘)+sin(30∘)) Bside=4π(a3/2)μ0I(21+21) Bside=2πa3μ0I(1) Bside=2πa3μ0I
-
Calculate total magnetic field: Since all 6 sides are identical and carry current in the same direction (e.g., counter-clockwise as per the arrows in the figure), the magnetic field produced by each side at the center will be in the same direction (out of the page, by the right-hand rule). Therefore, the total magnetic field at the center is the sum of the magnetic fields due to all 6 sides: Btotal=6×Bside Btotal=6×2πa3μ0I Btotal=πa33μ0I To rationalize the denominator, multiply numerator and denominator by 3: Btotal=3πa33μ0I Btotal=πa3μ0I
