Question

Number of triplets (a, b, c) of positive integer satisfying the equation

$\begin{vmatrix} a^3+1 & a^2b & a^2c \\ ab^2 & b^3+1 & b^2c \\ ac^2 & bc^2 & c^3+1 \end{vmatrix}$ = 11

is equal to

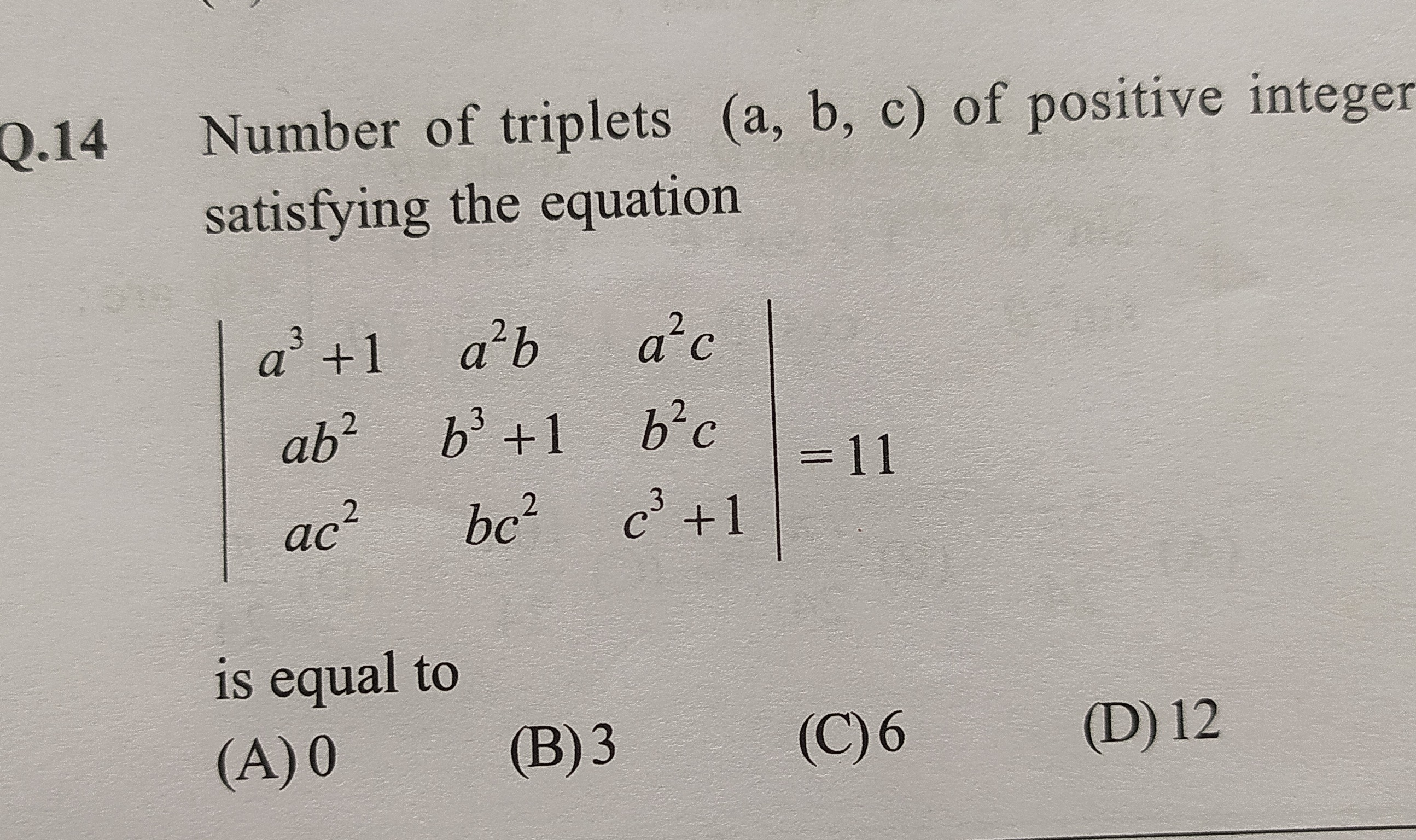
• A. 0
• B. 3
• C. 6
• D. 12

Answer 1

Answer: (B)

3

Answer 2

Solution:

We are given

$$\begin{vmatrix} a^3+1 & a^2b & a^2c \\ ab^2 & b^3+1 & b^2c \\ ac^2 & bc^2 & c^3+1 \end{vmatrix} = 11.$$

Step 1. Expand the Determinant

Expanding the determinant (by cofactor expansion or simplifying smartly) one obtains:

$$\text{Determinant} = a^3 + b^3 + c^3 + 1.$$

Step 2. Set Up the Equation

We have,

$$a^3 + b^3 + c^3 + 1 = 11 \quad \Longrightarrow \quad a^3 + b^3 + c^3 = 10.$$

Step 3. Find Positive Integer Solutions

Since $a$, $b$, and $c$ are positive integers, their cubes are:

$$1^3 = 1,\quad 2^3 = 8,\quad 3^3 = 27,\; \text{etc.}$$

To sum to 10, the only possibility is:

$$1 + 1 + 8 = 10.$$

Thus, one of the numbers must be $2$ (since $2^3 = 8$) and the other two must be $1$ (since $1^3 = 1$).

The ordered triplets are:

$$(2,1,1), \quad (1,2,1), \quad (1,1,2).$$

Step 4. Count the Triplets

There are exactly 3 triplets.

---

Explanation (Minimal):
The determinant simplifies to $a^3+b^3+c^3+1$. Setting this equal to 11 gives $a^3+b^3+c^3=10$. Since the only cubes below 10 are 1 and 8, we must have two 1's and one 8, leading to three ordered triplets.